Частные производные функции двух переменных.
Понятие и примеры решений

На данном уроке мы продолжим знакомство с функцией двух переменных и рассмотрим, пожалуй, самое распространенное тематическое задание – нахождение частных производных первого и второго порядка, а также полного дифференциала функции . Студенты-заочники, как правило, сталкиваются с частными производными на 1 курсе во 2 семестре. Причем, по моим наблюдениям, задание на нахождение частных производных практически всегда встречается на экзамене.

Для эффективного изучения нижеизложенного материала вам необходимо уметь более или менее уверенно находить «обычные» производные функции одной переменной. Научиться правильно обращаться с производными можно на уроках Как найти производную? и Производная сложной функции . Также нам потребуется таблица производных элементарных функций и правил дифференцирования, удобнее всего, если она будет под рукой в распечатанном виде. Раздобыть справочный материал можно на странице Математические формулы и таблицы .

Быстренько повторим понятие функции двух переменных , я постараюсь ограничиться самым минимумом. Функция двух переменных обычно записывается как , при этом переменные , называются независимыми переменными или аргументами .

Пример: – функция двух переменных.

Иногда используют запись . Также встречаются задания, где вместо буквы используется буква .

С геометрической точки зрения функция двух переменных чаще всего представляет собой поверхность трехмерного пространства (плоскость, цилиндр, шар, параболоид, гиперболоид и т. д.). Но, собственно, это уже больше аналитическая геометрия, а у нас на повестке дня математический анализ, который никогда не давал списывать мой вузовский преподаватель является моим «коньком».

Переходим к вопросу нахождения частных производных первого и второго порядков. Должен сообщить хорошую новость для тех, кто выпил несколько чашек кофе и настроился на невообразимо трудный материал: частные производные – это почти то же самое, что и «обычные» производные функции одной переменной .

Для частных производных справедливы все правила дифференцирования и таблица производных элементарных функций . Есть только пара небольших отличий, с которыми мы познакомимся прямо сейчас:

…да, кстати, для этой темы я таки создал маленькую pdf-книжку , которая позволит «набить руку» буквально за пару часов. Но, пользуясь сайтом, вы, безусловно, тоже получите результат – только может чуть медленнее:

Пример 1

Найти частные производные первого и второго порядка функции

Сначала найдем частные производные первого порядка. Их две.

Обозначения :
или – частная производная по «икс»
или – частная производная по «игрек»

Начнем с . Когда мы находим частную производную по «икс», то переменная считается константой (постоянным числом) .

Комментарии к выполненным действиям:

(1) Первое, что мы делаем при нахождении частной производной – заключаем всю функцию в скобки под штрих с подстрочным индексом .

Внимание, важно! Подстрочные индексы НЕ ТЕРЯЕМ по ходу решения. В данном случае, если вы где-нибудь нарисуете «штрих» без , то преподаватель, как минимум, может поставить рядом с заданием (сразу откусить часть балла за невнимательность).

(2) Используем правила дифференцирования , . Для простого примера, как этот, оба правила вполне можно применить на одном шаге. Обратите внимание на первое слагаемое: так как считается константой, а любую константу можно вынести за знак производной , то мы выносим за скобки. То есть в данной ситуации ничем не лучше обычного числа. Теперь посмотрим на третье слагаемое : здесь, наоборот, выносить нечего. Так как константа, то – тоже константа, и в этом смысле она ничем не лучше последнего слагаемого – «семерки».

(3) Используем табличные производные и .

(4) Упрощаем, или, как я люблю говорить, «причесываем» ответ.

Теперь . Когда мы находим частную производную по «игрек», то переменная считается константой (постоянным числом) .

(1) Используем те же правила дифференцирования , . В первом слагаемом выносим константу за знак производной, во втором слагаемом ничего вынести нельзя поскольку – уже константа.

(2) Используем таблицу производных элементарных функций. Мысленно поменяем в таблице все «иксы» на «игреки». То есть данная таблица рАвно справедлива и для (да и вообще почти для любой буквы) . В частности, используемые нами формулы выглядят так: и .

В чём смысл частных производных?

По своей сути частные производные 1-го порядка напоминают «обычную» производную :

– это функции , которые характеризуют скорость изменения функции в направлении осей и соответственно. Так, например, функция характеризует крутизну «подъёмов» и «склонов» поверхности в направлении оси абсцисс, а функция сообщает нам о «рельефе» этой же поверхности в направлении оси ординат.

! Примечание : здесь подразумеваются направления, которые параллельны координатным осям .

В целях лучшего понимания рассмотрим конкретную точку плоскости и вычислим в ней значение функции («высоту»):
– а теперь представьте, что вы здесь находитесь (НА САМОЙ поверхности).

Вычислим частную производную по «икс» в данной точке:

Отрицательный знак «иксовой» производной сообщает нам об убывании функции в точке по направлению оси абсцисс. Иными словами, если мы сделаем маленький-маленький (бесконечно малый) шажок в сторону острия оси (параллельно данной оси) , то спустимся вниз по склону поверхности.

Теперь узнаем характер «местности» по направлению оси ординат:

Производная по «игрек» положительна, следовательно, в точке по направлению оси функция возрастает . Если совсем просто, то здесь нас поджидает подъём в гору.

Кроме того, частная производная в точке характеризует скорость изменения функции по соответствующему направлению. Чем полученное значение больше по модулю – тем поверхность круче, и наоборот, чем оно ближе к нулю – тем поверхность более пологая. Так, в нашем примере «склон» по направлению оси абсцисс более крут, чем «гора» в направлении оси ординат.

Но то были два частных пути. Совершенно понятно, что из точки, в которой мы находимся, (и вообще из любой точки данной поверхности) мы можем сдвинуться и в каком-нибудь другом направлении. Таким образом, возникает интерес составить общую «навигационную карту», которая сообщала бы нам о «ландшафте» поверхности по возможности в каждой точке области определения данной функции по всем доступным путям. Об этом и других интересных вещах я расскажу на одном из следующих уроков, ну а пока что вернёмся к технической стороне вопроса.

Систематизируем элементарные прикладные правила:

1) Когда мы дифференцируем по , то переменная считается константой.

2) Когда же дифференцирование осуществляется по , то константой считается .

3) Правила и таблица производных элементарных функций справедливы и применимы для любой переменной (, либо какой-нибудь другой), по которой ведется дифференцирование.

Шаг второй. Находим частные производные второго порядка. Их четыре.

Обозначения :
или – вторая производная по «икс»
или – вторая производная по «игрек»
или – смешанная производная «икс по игрек»
или – смешанная производная «игрек по икс»

Со второй производной нет никаких проблем. Говоря простым языком, вторая производная – это производная от первой производной .

Для удобства я перепишу уже найденные частные производные первого порядка:

Сначала найдем смешанные производные:

Как видите, всё просто: берем частную производную и дифференцируем ее еще раз, но в данном случае – уже по «игрек».

Аналогично:

В практических примерах можно ориентироваться на следующее равенство :

Таким образом, через смешанные производные второго порядка очень удобно проверить, а правильно ли мы нашли частные производные первого порядка.

Находим вторую производную по «икс».
Никаких изобретений, берем и дифференцируем её по «икс» еще раз:

Аналогично:

Следует отметить, что при нахождении , нужно проявить повышенное внимание , так как никаких чудесных равенств для их проверки не существует.

Вторые производные также находят широкое практическое применение, в частности, они используются в задаче отыскания экстремумов функции двух переменных . Но всему своё время:

Пример 2

Вычислить частные производные первого порядка функции в точке . Найти производные второго порядка.

Это пример для самостоятельного решения (ответы в конце урока). Если возникли трудности с дифференцированием корней, вернитесь к уроку Как найти производную? А вообще, довольно скоро вы научитесь находить подобные производные «с лёту».

Набиваем руку на более сложных примерах:

Пример 3

Проверить, что . Записать полный дифференциал первого порядка .

Решение: Находим частные производные первого порядка:

Обратите внимание на подстрочный индекс: , рядом с «иксом» не возбраняется в скобках записывать, что – константа. Данная пометка может быть очень полезна для начинающих, чтобы легче было ориентироваться в решении.

Дальнейшие комментарии:

(1) Выносим все константы за знак производной. В данном случае и , а, значит, и их произведение считается постоянным числом.

(2) Не забываем, как правильно дифференцировать корни.

(1) Выносим все константы за знак производной, в данной случае константой является .

(2) Под штрихом у нас осталось произведение двух функций, следовательно, нужно использовать правило дифференцирования произведения .

(3) Не забываем, что – это сложная функция (хотя и простейшая из сложных). Используем соответствующее правило: .

Теперь находим смешанные производные второго порядка:

Значит, все вычисления выполнены верно.

Запишем полный дифференциал . В контексте рассматриваемого задания не имеет смысла рассказывать, что такое полный дифференциал функции двух переменных. Важно, что этот самый дифференциал очень часто требуется записать в практических задачах.

Полный дифференциал первого порядка функции двух переменных имеет вид:

В данном случае:

То есть, в формулу нужно тупо просто подставить уже найденные частные производные первого порядка. Значки дифференциалов и в этой и похожих ситуациях по возможности лучше записывать в числителях:

И по неоднократным просьбам читателей, полный дифференциал второго порядка .

Он выглядит так:

ВНИМАТЕЛЬНО найдём «однобуквенные» производные 2-го порядка:

и запишем «монстра», аккуратно «прикрепив» квадраты , произведение и не забыв удвоить смешанную производную:

Ничего страшного, если что-то показалось трудным, к производным всегда можно вернуться позже, после того, как поднимите технику дифференцирования:

Пример 4

Найти частные производные первого порядка функции . Проверить, что . Записать полный дифференциал первого порядка .

Рассмотрим серию примеров со сложными функциями:

Пример 5

Найти частные производные первого порядка функции .

Решение:

Пример 6

Найти частные производные первого порядка функции .
Записать полный дифференциал .

Это пример для самостоятельного решения (ответ в конце урока). Полное решение не привожу, так как оно достаточно простое

Довольно часто все вышерассмотренные правила применяются в комбинации.

Пример 7

Найти частные производные первого порядка функции .

(1) Используем правило дифференцирования суммы

(2) Первое слагаемое в данном случае считается константой, поскольку в выражении нет ничего, зависящего от «икс» – только «игреки». Знаете, всегда приятно, когда дробь удается превратить в ноль). Для второго слагаемого применяем правило дифференцирования произведения. Кстати, в этом смысле ничего бы не изменилось, если бы вместо была дана функция – важно, что здесь произведение двух функций, КАЖДАЯ из которых зависит от «икс» , а поэтому, нужно использовать правило дифференцирования произведения. Для третьего слагаемого применяем правило дифференцирования сложной функции.

(1) В первом слагаемом и в числителе и в знаменателе содержится «игрек», следовательно, нужно использовать правило дифференцирования частного: . Второе слагаемое зависит ТОЛЬКО от «икс», значит, считается константой и превращается в ноль. Для третьего слагаемого используем правило дифференцирования сложной функции.

Для тех читателей, которые мужественно добрались почти до конца урока, расскажу старый мехматовский анекдот для разрядки:

Однажды в пространстве функций появилась злобная производная и как пошла всех дифференцировать. Все функции разбегаются кто куда, никому не хочется превращаться! И только одна функция никуда не убегает. Подходит к ней производная и спрашивает:

– А почему это ты от меня никуда не убегаешь?

– Ха. А мне всё равно, ведь я «е в степени икс», и ты со мной ничего не сделаешь!

На что злобная производная с коварной улыбкой отвечает:

– Вот здесь ты ошибаешься, я тебя продифференцирую по «игрек», так что быть тебе нулем.

Кто понял анекдот, тот освоил производные, минимум, на «тройку»).

Пример 8

Найти частные производные первого порядка функции .

Это пример для самостоятельного решения. Полное решение и образец оформления задачи – в конце урока.

Ну вот почти и всё. Напоследок не могу не обрадовать любителей математики еще одним примером. Дело даже не в любителях, у всех разный уровень математической подготовки – встречаются люди (и не так уж редко), которые любят потягаться с заданиями посложнее. Хотя, последний на данном уроке пример не столько сложный, сколько громоздкий с точки зрения вычислений.

Рассмотрим функцию от двух переменных:

Поскольку переменные $x$ и $y$ являются независимыми, для такой функции можно ввести понятие частной производной:

Частная производная функции $f$ в точке $M=\left({{x}_{0}};{{y}_{0}} \right)$ по переменной $x$ — это предел

\[{{{f}"}_{x}}=\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{f\left({{x}_{0}}+\Delta x;{{y}_{0}} \right)}{\Delta x}\]

Аналогично можно определить частную производную по переменной $y$ :

\[{{{f}"}_{y}}=\underset{\Delta y\to 0}{\mathop{\lim }}\,\frac{f\left({{x}_{0}};{{y}_{0}}+\Delta y \right)}{\Delta y}\]

Другими словами, чтобы найти частную производную функции нескольких переменных, нужно зафиксировать все остальные переменные, кроме искомой, а затем найти обычную производную по этой искомой переменной.

Отсюда вытекает основной приём для вычисления таких производных: просто считайте, что все переменные, кроме данной, являются константой, после чего дифференцируйте функцию так, как дифференцировали бы «обычную» — с одной переменной. Например:

$\begin{align}& {{\left({{x}^{2}}+10xy \right)}_{x}}^{\prime }={{\left({{x}^{2}} \right)}^{\prime }}_{x}+10y\cdot {{\left(x \right)}^{\prime }}_{x}=2x+10y, \\& {{\left({{x}^{2}}+10xy \right)}_{y}}^{\prime }={{\left({{x}^{2}} \right)}^{\prime }}_{y}+10x\cdot {{\left(y \right)}^{\prime }}_{y}=0+10x=10x. \\\end{align}$

Очевидно, что частные производные по разным переменным дают разные ответы — это нормально. Куда важнее понимать, почему, скажем, в первом случае мы спокойно вынесли $10y$ из-под знака производной, а во втором — вовсе обнулили первое слагаемое. Всё это происходит из-за того, что все буквы, кроме переменной, по которой идёт дифференцирование, считаются константами: их можно выносить, «сжигать» и т.д.

Что такое «частная производная»?

Сегодня мы поговорим о функциях нескольких переменных и о частных производных от них. Во-первых, что такое функция нескольких переменных? До сих пор мы привыкли считать функцию как $y\left(x \right)$ или $t\left(x \right)$, или любую переменную и одну-единственную функцию от нее. Теперь же функция у нас будет одна, а переменных несколько. При изменении $y$ и $x$ значение функции будет меняться. Например, если $x$ увеличится в два раза, значение функции поменяется, при этом если $x$ поменяется, а $y$ не изменится, значение функции точно так же изменится.

Разумеется, функцию от нескольких переменных, точно так же как и от одной переменной, можно дифференцировать. Однако поскольку переменных несколько, то и дифференцировать можно по разным переменным. При этом возникают специфические правила, которых не было при дифференцировании одной переменной.

Прежде всего, когда мы считаем производную функции от какой-либо переменной, то обязаны указывать, по какой именно переменной мы считаем производную — это и называется частной производной. Например, у нас функция от двух переменных, и мы можем посчитать ее как по $x$, так и по $y$ — две частных производных у каждой из переменных.

Во-вторых, как только мы зафиксировали одну из переменных и начинаем считать частную производную именно по ней, то все остальные, входящие в эту функцию, считаются константами. Например, в $z\left(xy \right)$, если мы считаем частную производную по $x$, то везде, где мы встречаем $y$, мы считаем ее константой и обращаемся с ней именно как с константой. В частности при вычислении производной произведения мы можем выносить $y$ за скобку (у нас же константа), а при вычислении производной суммы, если у нас где-то получается производная от выражения, содержащего $y$ и не содержащего $x$, то производная этого выражения будет равна «нулю» как производная константы.

На первый взгляд может показаться, что я рассказываю о чем-то сложном, и многие ученики по началу путаются. Однако ничего сверхъестественного в частных производных нет, и сейчас мы убедимся в этом на примере конкретных задач.

Задачи с радикалами и многочленами

Задача № 1

Чтобы не терять время зря, с самого начала начнем с серьезных примеров.

Для начала напомню такую формулу:

Это стандартное табличное значение, которое мы знаем из стандартного курса.

В этом случае производная $z$ считается следующим образом:

\[{{{z}"}_{x}}={{\left(\sqrt{\frac{y}{x}} \right)}^{\prime }}_{x}=\frac{1}{2\sqrt{\frac{y}{x}}}{{\left(\frac{y}{x} \right)}^{\prime }}_{x}\]

Давайте еще раз, поскольку под корнем стоит не $x$, а некое другое выражение, в данном случае $\frac{y}{x}$, то сначала мы воспользуемся стандартным табличным значением, а затем, поскольку под корнем стоит не $x$, а другое выражение, нам необходимо домножить нашу производную на еще одну из этого выражения по той же самой переменной. Давайте для начала посчитаем следующее:

\[{{\left(\frac{y}{x} \right)}^{\prime }}_{x}=\frac{{{{{y}"}}_{x}}\cdot x-y\cdot {{{{x}"}}_{x}}}{{{x}^{2}}}=\frac{0\cdot x-y\cdot 1}{{{x}^{2}}}=-\frac{y}{{{x}^{2}}}\]

Возвращаемся к нашему выражению и записываем:

\[{{{z}"}_{x}}={{\left(\sqrt{\frac{y}{x}} \right)}^{\prime }}_{x}=\frac{1}{2\sqrt{\frac{y}{x}}}{{\left(\frac{y}{x} \right)}^{\prime }}_{x}=\frac{1}{2\sqrt{\frac{y}{x}}}\cdot \left(-\frac{y}{{{x}^{2}}} \right)\]

В принципе, это все. Однако оставлять ее в таком виде неправильно: такую конструкцию неудобно использовать для дальнейших вычислений, поэтому давайте ее немного преобразуем:

\[\frac{1}{2\sqrt{\frac{y}{x}}}\cdot \left(-\frac{y}{{{x}^{2}}} \right)=\frac{1}{2}\cdot \sqrt{\frac{x}{y}}\cdot \frac{y}{{{x}^{2}}}=\]

\[=-\frac{1}{2}\cdot \sqrt{\frac{x}{y}}\cdot \sqrt{\frac{{{y}^{2}}}{{{x}^{4}}}}=-\frac{1}{2}\sqrt{\frac{x\cdot {{y}^{2}}}{y\cdot {{x}^{4}}}}=-\frac{1}{2}\sqrt{\frac{y}{{{x}^{3}}}}\]

Ответ найден. Теперь займемся $y$:

\[{{{z}"}_{y}}={{\left(\sqrt{\frac{y}{x}} \right)}^{\prime }}_{y}=\frac{1}{2\sqrt{\frac{y}{x}}}\cdot {{\left(\frac{y}{x} \right)}^{\prime }}_{y}\]

Выпишем отдельно:

\[{{\left(\frac{y}{x} \right)}^{\prime }}_{y}=\frac{{{{{y}"}}_{y}}\cdot x-y\cdot {{{{x}"}}_{y}}}{{{x}^{2}}}=\frac{1\cdot x-y\cdot 0}{{{x}^{2}}}=\frac{1}{x}\]

Теперь записываем:

\[{{{z}"}_{y}}={{\left(\sqrt{\frac{y}{x}} \right)}^{\prime }}_{y}=\frac{1}{2\sqrt{\frac{y}{x}}}\cdot {{\left(\frac{y}{x} \right)}^{\prime }}_{y}=\frac{1}{2\sqrt{\frac{y}{x}}}\cdot \frac{1}{x}=\]

\[=\frac{1}{2}\cdot \sqrt{\frac{x}{y}}\cdot \sqrt{\frac{1}{{{x}^{2}}}}=\frac{1}{2}\sqrt{\frac{x}{y\cdot {{x}^{2}}}}=\frac{1}{2\sqrt{xy}}\]

Все сделано.

Задача № 2

Этот пример одновременно и проще, и сложней, чем предыдущий. Сложнее, потому что здесь больше действий, а проще, потому что здесь нет корня и, кроме того, функция симметрична относительно $x$ и $y$, т.е. если мы поменяем $x$ и $y$ местами, формула от этого не изменится. Это замечание в дальнейшем упростит нам вычисление частной производной, т.е. достаточно посчитать одну из них, а во второй просто поменять местами $x$ и $y$.

Приступаем к делу:

\[{{{z}"}_{x}}={{\left(\frac{xy}{{{x}^{2}}+{{y}^{2}}+1} \right)}^{\prime }}_{x}=\frac{{{\left(xy \right)}^{\prime }}_{x}\left({{x}^{2}}+{{y}^{2}}+1 \right)-xy{{\left({{x}^{2}}+{{y}^{2}}+1 \right)}^{\prime }}_{x}}{{{\left({{x}^{2}}+{{y}^{2}}+1 \right)}^{2}}}\]

Давайте посчитаем:

\[{{\left(xy \right)}^{\prime }}_{x}=y\cdot {{\left(x \right)}^{\prime }}=y\cdot 1=y\]

Однако многим ученикам такая запись непонятна, поэтому запишем вот так:

\[{{\left(xy \right)}^{\prime }}_{x}={{\left(x \right)}^{\prime }}_{x}\cdot y+x\cdot {{\left(y \right)}^{\prime }}_{x}=1\cdot y+x\cdot 0=y\]

Таким образом, мы еще раз убеждаемся в универсальности алгоритма частных производных: каким бы мы образом их не считали, если все правила применяются верно, ответ будет один и тот же.

Теперь давайте разберемся еще с одной частной производной из нашей большой формулы:

\[{{\left({{x}^{2}}+{{y}^{2}}+1 \right)}^{\prime }}_{x}={{\left({{x}^{2}} \right)}^{\prime }}_{x}+{{\left({{y}^{2}} \right)}^{\prime }}_{x}+{{{1}"}_{x}}=2x+0+0\]

Подставим полученные выражения в нашу формулу и получим:

\[\frac{{{\left(xy \right)}^{\prime }}_{x}\left({{x}^{2}}+{{y}^{2}}+1 \right)-xy{{\left({{x}^{2}}+{{y}^{2}}+1 \right)}^{\prime }}_{x}}{{{\left({{x}^{2}}+{{y}^{2}}+1 \right)}^{2}}}=\]

\[=\frac{y\cdot \left({{x}^{2}}+{{y}^{2}}+1 \right)-xy\cdot 2x}{{{\left({{x}^{2}}+{{y}^{2}}+1 \right)}^{2}}}=\]

\[=\frac{y\left({{x}^{2}}+{{y}^{2}}+1-2{{x}^{2}} \right)}{{{\left({{x}^{2}}+{{y}^{2}}+1 \right)}^{2}}}=\frac{y\left({{y}^{2}}-{{x}^{2}}+1 \right)}{{{\left({{x}^{2}}+{{y}^{2}}+1 \right)}^{2}}}\]

По $x$ посчитано. А чтобы посчитать $y$ от того же самого выражения, давайте не будем выполнять всю ту же последовательность действий, а воспользуемся симметрией нашего исходного выражения — мы просто заменим в нашем исходном выражении все $y$ на $x$ и наоборот:

\[{{{z}"}_{y}}=\frac{x\left({{x}^{2}}-{{y}^{2}}+1 \right)}{{{\left({{x}^{2}}+{{y}^{2}}+1 \right)}^{2}}}\]

За счет симметрии мы посчитали это выражение гораздо быстрее.

Нюансы решения

Для частных производных работают все стандартные формулы, которые мы используем для обычных, а именно, производная частного. При этом, однако, возникают свои специфические особенности: если мы считаем частную производную $x$, то когда мы получаем ее по $x$, то рассматриваем ее как константу, и поэтому ее производная будет равна «нулю».

Как и в случае с обычными производными, частную (одну и ту же) можно посчитать несколькими различными способами. Например, ту же конструкцию, которую мы только что посчитали, можно переписать следующим образом:

\[{{\left(\frac{y}{x} \right)}^{\prime }}_{x}=y\cdot {{\left(\frac{1}{x} \right)}^{\prime }}_{x}=-y\frac{1}{{{x}^{2}}}\]

\[{{\left(xy \right)}^{\prime }}_{x}=y\cdot {{{x}"}_{x}}=y\cdot 1=y\]

Вместе с тем, с другой стороны, можно использовать формулу от производной суммы. Как мы знаем, она равна сумме производных. Например, запишем следующее:

\[{{\left({{x}^{2}}+{{y}^{2}}+1 \right)}^{\prime }}_{x}=2x+0+0=2x\]

Теперь, зная все это, давайте попробуем поработать с более серьезными выражениями, поскольку настоящие частные производные не ограничиваются одними лишь многочленами и корнями: там встречаются и тригонометрия, и логарифмы, и показательная функция. Сейчас этим и займемся.

Задачи с тригонометрическими функциями и логарифмами

Задача № 1

Запишем следующие стандартные формулы:

\[{{\left(\sqrt{x} \right)}^{\prime }}_{x}=\frac{1}{2\sqrt{x}}\]

\[{{\left(\cos x \right)}^{\prime }}_{x}=-\sin x\]

Вооружившись этими знаниями, попробуем решить:

\[{{{z}"}_{x}}={{\left(\sqrt{x}\cdot \cos \frac{x}{y} \right)}^{\prime }}_{x}={{\left(\sqrt{x} \right)}^{\prime }}_{x}\cdot \cos \frac{x}{y}+\sqrt{x}\cdot {{\left(\cos \frac{x}{y} \right)}^{\prime }}_{x}=\]

Отдельно выпишем одну переменную:

\[{{\left(\cos \frac{x}{y} \right)}^{\prime }}_{x}=-\sin \frac{x}{y}\cdot {{\left(\frac{x}{y} \right)}^{\prime }}_{x}=-\frac{1}{y}\cdot \sin \frac{x}{y}\]

Возвращаемся к нашей конструкции:

\[=\frac{1}{2\sqrt{x}}\cdot \cos \frac{x}{y}+\sqrt{x}\cdot \left(-\frac{1}{y}\cdot \sin \frac{x}{y} \right)=\frac{1}{2\sqrt{x}}\cdot \cos \frac{x}{y}-\frac{\sqrt{x}}{y}\cdot \sin \frac{x}{y}\]

Все, по $x$ мы нашли, теперь давайте займемся вычислениями по $y$:

\[{{{z}"}_{y}}={{\left(\sqrt{x}\cdot \cos \frac{x}{y} \right)}^{\prime }}_{y}={{\left(\sqrt{x} \right)}^{\prime }}_{y}\cdot \cos \frac{x}{y}+\sqrt{x}\cdot {{\left(\cos \frac{x}{y} \right)}^{\prime }}_{y}=\]

Опять же посчитаем одно выражение:

\[{{\left(\cos \frac{x}{y} \right)}^{\prime }}_{y}=-\sin \frac{x}{y}\cdot {{\left(\frac{x}{y} \right)}^{\prime }}_{y}=-\sin \frac{x}{y}\cdot x\cdot \left(-\frac{1}{{{y}^{2}}} \right)\]

Возвращаемся к исходному выражению и продолжаем решение:

\[=0\cdot \cos \frac{x}{y}+\sqrt{x}\cdot \frac{x}{{{y}^{2}}}\sin \frac{x}{y}=\frac{x\sqrt{x}}{{{y}^{2}}}\cdot \sin \frac{x}{y}\]

Все сделано.

Задача № 2

Запишем необходимую нам формулу:

\[{{\left(\ln x \right)}^{\prime }}_{x}=\frac{1}{x}\]

Теперь посчитаем по $x$:

\[{{{z}"}_{x}}={{\left(\ln \left(x+\ln y \right) \right)}^{\prime }}_{x}=\frac{1}{x+\ln y}.{{\left(x+\ln y \right)}^{\prime }}_{x}=\]

\[=\frac{1}{x+\ln y}\cdot \left(1+0 \right)=\frac{1}{x+\ln y}\]

По $x$ найдено. Считаем по $y$:

\[{{{z}"}_{y}}={{\left(\ln \left(x+\ln y \right) \right)}^{\prime }}_{y}=\frac{1}{x+\ln y}.{{\left(x+\ln y \right)}^{\prime }}_{y}=\]

\[=\frac{1}{x+\ln y}\left(0+\frac{1}{y} \right)=\frac{1}{y\left(x+\ln y \right)}\]

Задача решена.

Нюансы решения

Итак, от какой бы функции мы не брали частную производную, правила остаются одними и теми же, независимо от того, работаем ли мы с тригонометрией, с корнями или с логарифмами.

Неизменными остаются классические правила работы со стандартными производными, а именно, производная суммы и разности, частного и сложной функции.

Последняя формула чаще всего и встречается при решении задач с частными производными. Мы встречаемся с ними практически везде. Ни одной задачи еще не было, чтобы там нам она не попадалась. Но какой бы мы формулой не воспользовались, нам все равно добавляется еще одно требование, а именно, особенность работы с частными производными. Как только мы фиксируем одну переменную, все остальные оказываются константами. В частности, если мы считаем частную производную выражения $\cos \frac{x}{y}$ по $y$, то именно $y$ и является переменной, а $x$ везде остается константой. То же самое работает и наоборот. Ее можно выносить за знак производной, а производная от самой константы будет равна «нулю».

Все это приводит к тому, что частные производные от одного и того же выражения, но по разным переменным могут выглядеть совершенно по-разному. Например, посмотрим такие выражения:

\[{{\left(x+\ln y \right)}^{\prime }}_{x}=1+0=1\]

\[{{\left(x+\ln y \right)}^{\prime }}_{y}=0+\frac{1}{y}=\frac{1}{y}\]

Задачи с показательными функциями и логарифмами

Задача № 1

Для начала запишем такую формулу:

\[{{\left({{e}^{x}} \right)}^{\prime }}_{x}={{e}^{x}}\]

Зная этот факт, а также производную сложной функции, давайте попробуем посчитать. Я сейчас решу двумя различными способами. Первый и самый очевидный — это производная произведения:

\[{{{z}"}_{x}}={{\left({{e}^{x}}\cdot {{e}^{\frac{x}{y}}} \right)}^{\prime }}_{x}={{\left({{e}^{x}} \right)}^{\prime }}_{x}\cdot {{e}^{\frac{x}{y}}}+{{e}^{x}}\cdot {{\left({{e}^{\frac{x}{y}}} \right)}^{\prime }}_{x}=\]

\[={{e}^{x}}\cdot {{e}^{\frac{x}{y}}}+{{e}^{x}}\cdot {{e}^{\frac{x}{y}}}\cdot {{\left(\frac{x}{y} \right)}^{\prime }}_{x}=\]

Давайте решим отдельно следующее выражение:

\[{{\left(\frac{x}{y} \right)}^{\prime }}_{x}=\frac{{{{{x}"}}_{x}}\cdot y-x.{{{{y}"}}_{x}}}{{{y}^{2}}}=\frac{1\cdot y-x\cdot 0}{{{y}^{2}}}=\frac{y}{{{y}^{2}}}=\frac{1}{y}\]

Возвращаемся к нашей исходной конструкции и продолжаем решение:

\[={{e}^{x}}\cdot {{e}^{\frac{x}{y}}}+{{e}^{x}}\cdot {{e}^{\frac{x}{y}}}\cdot \frac{1}{y}={{e}^{x}}\cdot {{e}^{\frac{x}{y}}}\left(1+\frac{1}{y} \right)\]

Все, по $x$ посчитано.

Однако как я и обещал, сейчас постараемся посчитать эту же частную производную другим способом. Для этого заметим следующее:

\[{{e}^{x}}\cdot {{e}^{\frac{x}{y}}}={{e}^{x+\frac{x}{y}}}\]

В этом запишем так:

\[{{\left({{e}^{x}}\cdot {{e}^{\frac{x}{y}}} \right)}^{\prime }}_{x}={{\left({{e}^{x+\frac{x}{y}}} \right)}^{\prime }}_{x}={{e}^{x+\frac{x}{y}}}\cdot {{\left(x+\frac{x}{y} \right)}^{\prime }}_{x}={{e}^{x+\frac{x}{y}}}\cdot \left(1+\frac{1}{y} \right)\]

В результате мы получили точно такой же ответ, однако объем вычислений оказался меньшим. Для этого достаточно было заметить, что при произведении показатели можно складывать.

Теперь посчитаем по $y$:

\[{{{z}"}_{y}}={{\left({{e}^{x}}\cdot {{e}^{\frac{x}{y}}} \right)}^{\prime }}_{y}={{\left({{e}^{x}} \right)}^{\prime }}_{y}\cdot {{e}^{\frac{x}{y}}}+{{e}^{x}}\cdot {{\left({{e}^{\frac{x}{y}}} \right)}^{\prime }}_{y}=\]

\[=0\cdot {{e}^{\frac{x}{y}}}+{{e}^{x}}\cdot {{e}^{\frac{x}{y}}}\cdot {{\left(\frac{x}{y} \right)}^{\prime }}_{y}=\]

Давайте решим одно выражение отдельно:

\[{{\left(\frac{x}{y} \right)}^{\prime }}_{y}=\frac{{{{{x}"}}_{y}}\cdot y-x\cdot {{{{y}"}}_{y}}}{{{y}^{2}}}=\frac{0-x\cdot 1}{{{y}^{2}}}=-\frac{1}{{{y}^{2}}}=-\frac{x}{{{y}^{2}}}\]

Продолжим решение нашей исходной конструкции:

\[={{e}^{x}}\cdot {{e}^{\frac{x}{y}}}\cdot \left(-\frac{x}{{{y}^{2}}} \right)=-\frac{x}{{{y}^{2}}}\cdot {{e}^{x}}\cdot {{e}^{\frac{x}{y}}}\]

Разумеется, эту же производную можно было бы посчитать вторым способом, ответ получился бы таким же.

Задача № 2

Посчитаем по $x$:

\[{{{z}"}_{x}}={{\left(x \right)}_{x}}\cdot \ln \left({{x}^{2}}+y \right)+x\cdot {{\left(\ln \left({{x}^{2}}+y \right) \right)}^{\prime }}_{x}=\]

Давайте посчитаем одно выражение отдельно:

\[{{\left(\ln \left({{x}^{2}}+y \right) \right)}^{\prime }}_{x}=\frac{1}{{{x}^{2}}+y}\cdot {{\left({{x}^{2}}+y \right)}^{\prime }}_{x}=\frac{2x}{{{x}^{2}}+y}\]

Продолжим решение исходной конструкции: $$

Вот такой ответ.

Осталось по аналогии найти по $y$:

\[{{{z}"}_{y}}={{\left(x \right)}^{\prime }}_{y}.\ln \left({{x}^{2}}+y \right)+x\cdot {{\left(\ln \left({{x}^{2}}+y \right) \right)}^{\prime }}_{y}=\]

Одно выражение посчитаем как всегда отдельно:

\[{{\left({{x}^{2}}+y \right)}^{\prime }}_{y}={{\left({{x}^{2}} \right)}^{\prime }}_{y}+{{{y}"}_{y}}=0+1=1\]

Продолжаем решение основной конструкции:

Все посчитано. Как видите, в зависимости от того, какая переменная берется для дифференцирования, ответы получаются совершенно разные.

Нюансы решения

Вот яркий пример того, как производную одной и той же функции можно посчитать двумя различными способами. Вот смотрите:

\[{{{z}"}_{x}}=\left({{e}^{x}}\cdot {{e}^{\frac{x}{y}}} \right)={{\left({{e}^{x}} \right)}^{\prime }}_{x}\cdot {{e}^{\frac{x}{y}}}+{{e}^{x}}\cdot {{\left({{e}^{\frac{x}{y}}} \right)}^{\prime }}_{x}=\]

\[={{e}^{x}}\cdot {{e}^{\frac{x}{y}}}+{{e}^{x}}\cdot {{e}^{\frac{x}{y}}}\cdot \frac{1}{y}={{e}^{x}}\cdot {{e}^{^{\frac{x}{y}}}}\left(1+\frac{1}{y} \right)\]

\[{{{z}"}_{x}}={{\left({{e}^{x}}.{{e}^{\frac{x}{y}}} \right)}^{\prime }}_{x}={{\left({{e}^{x+\frac{x}{y}}} \right)}^{\prime }}_{x}={{e}^{x+\frac{x}{y}}}.{{\left(x+\frac{x}{y} \right)}^{\prime }}_{x}=\]

\[={{e}^{x}}\cdot {{e}^{^{\frac{x}{y}}}}\left(1+\frac{1}{y} \right)\]

При выборе разных путей, объем вычислений может быть разный, но ответ, если все выполнено верно, получится одним и тем же. Это касается как классических, так и частных производных. При этом еще раз напоминаю: в зависимости от того, по какой переменной идет взятие производной, т.е. дифференцирование, ответ может получиться совершенно разный. Посмотрите:

\[{{\left(\ln \left({{x}^{2}}+y \right) \right)}^{\prime }}_{x}=\frac{1}{{{x}^{2}}+y}\cdot {{\left({{x}^{2}}+y \right)}^{\prime }}_{x}=\frac{1}{{{x}^{2}}+y}\cdot 2x\]

\[{{\left(\ln \left({{x}^{2}}+y \right) \right)}^{\prime }}_{y}=\frac{1}{{{x}^{2}}+y}\cdot {{\left({{x}^{2}}+y \right)}^{\prime }}_{y}=\frac{1}{{{x}^{2}}+y}\cdot 1\]

В заключение для закрепления всего этого материала давайте попробуем посчитать еще два примера.

Задачи с тригонометрической функция и функцией с тремя переменными

Задача № 1

Давайте запишем такие формулы:

\[{{\left({{a}^{x}} \right)}^{\prime }}={{a}^{x}}\cdot \ln a\]

\[{{\left({{e}^{x}} \right)}^{\prime }}={{e}^{x}}\]

Давайте теперь решать наше выражение:

\[{{{z}"}_{x}}={{\left({{3}^{x\sin y}} \right)}^{\prime }}_{x}={{3}^{x.\sin y}}\cdot \ln 3\cdot {{\left(x\cdot \sin y \right)}^{\prime }}_{x}=\]

Отдельно посчитаем такую конструкцию:

\[{{\left(x\cdot \sin y \right)}^{\prime }}_{x}={{{x}"}_{x}}\cdot \sin y+x{{\left(\sin y \right)}^{\prime }}_{x}=1\cdot \sin y+x\cdot 0=\sin y\]

Продолжаем решать исходное выражение:

\[={{3}^{x\sin y}}\cdot \ln 3\cdot \sin y\]

Это окончательный ответ частной переменной по $x$. Теперь посчитаем по $y$:

\[{{{z}"}_{y}}={{\left({{3}^{x\sin y}} \right)}^{\prime }}_{y}={{3}^{x\sin y}}\cdot \ln 3\cdot {{\left(x\sin y \right)}^{\prime }}_{y}=\]

Решим одно выражение отдельно:

\[{{\left(x\cdot \sin y \right)}^{\prime }}_{y}={{{x}"}_{y}}\cdot \sin y+x{{\left(\sin y \right)}^{\prime }}_{y}=0\cdot \sin y+x\cdot \cos y=x\cdot \cos y\]

Решаем до конца нашу конструкцию:

\[={{3}^{x\cdot \sin y}}\cdot \ln 3\cdot x\cos y\]

Задача № 2

На первый взгляд этот пример может показаться достаточно сложным, потому что здесь три переменных. На самом деле, это одна из самых простых задач в сегодняшнем видеоуроке.

Находим по $x$:

\[{{{t}"}_{x}}={{\left(x{{e}^{y}}+y{{e}^{z}} \right)}^{\prime }}_{x}={{\left(x\cdot {{e}^{y}} \right)}^{\prime }}_{x}+{{\left(y\cdot {{e}^{z}} \right)}^{\prime }}_{x}=\]

\[={{\left(x \right)}^{\prime }}_{x}\cdot {{e}^{y}}+x\cdot {{\left({{e}^{y}} \right)}^{\prime }}_{x}=1\cdot {{e}^{y}}+x\cdot o={{e}^{y}}\]

Теперь разберемся с $y$:

\[{{{t}"}_{y}}={{\left(x\cdot {{e}^{y}}+y\cdot {{e}^{z}} \right)}^{\prime }}_{y}={{\left(x\cdot {{e}^{y}} \right)}^{\prime }}_{y}+{{\left(y\cdot {{e}^{z}} \right)}^{\prime }}_{y}=\]

\[=x\cdot {{\left({{e}^{y}} \right)}^{\prime }}_{y}+{{e}^{z}}\cdot {{\left(y \right)}^{\prime }}_{y}=x\cdot {{e}^{y}}+{{e}^{z}}\]

Мы нашли ответ.

Теперь остается найти по $z$:

\[{{{t}"}_{z}}={{\left(x\cdot {{e}^{y}}+{{y}^{z}} \right)}^{\prime }}_{z}={{\left(x\cdot {{e}^{y}} \right)}^{\prime }}_{z}+{{\left(y\cdot {{e}^{z}} \right)}^{\prime }}_{z}=0+y\cdot {{\left({{e}^{z}} \right)}^{\prime }}_{z}=y\cdot {{e}^{z}}\]

Мы посчитали третью производную, на чем решение второй задачи полностью завершено.

Нюансы решения

Как видите, ничего сложного в этих двух примерах нет. Единственное, в чем мы убедились, так это в том, что производная сложной функции применяется часто и в зависимости от того, какую частную производную мы считаем, мы получаем разные ответы.

В последней задаче нам было предложено разобраться с функцией сразу от трех переменных. Ничего страшного в этом нет, однако в самом конце мы убедились, что все они друг от друга существенно отличаются.

Ключевые моменты

Окончательные выводы из сегодняшнего видеоурока следующие:

1. Частные производные считаются так же, как и обычные, при этом, чтобы считать частную производную по одной переменной, все остальные переменные, входящие в данную функцию, мы принимаем за константы.
2. При работе с частными производными мы используем все те же стандартные формулы, что и с обычными производными: сумму, разность, производную произведения и частного и, разумеется, производную сложной функции.

Конечно, просмотра одного этого видеоурока недостаточно, чтобы полностью разобраться в этой теме, поэтому прямо сейчас на моем сайте именно к этому видео есть комплект задач, посвященных именно сегодняшней теме — заходите, скачивайте, решайте эти задачи и сверяйтесь с ответом. И после этого никаких проблем с частными производными ни на экзаменах, ни на самостоятельных работах у вас не будет. Конечно, это далеко не последний урок по высшей математике, поэтому заходите на наш сайт, добавляйтесь ВКонтакте, подписывайтесь на YouTube, ставьте лайки и оставайтесь с нами!

Рассмотрены примеры вычисления производных высших порядков явных функций. Даны полезные формулы для вычисления производных n-го порядка.

Содержание

Определение производных высших порядков

Здесь мы рассматриваем случай, когда переменная y зависит от переменной x явным образом:
.
Дифференцируя функцию по переменной x , получаем производную первого порядка, или просто производную:
.
В результате получаем новую функцию , которая является производной функции . Дифференцируя эту новую функцию по переменной x , получаем производную второго порядка:
.
Дифференцируя функцию , получаем производную третьего порядка:
.
И так далее. Дифференцируя исходную функцию n раз, получаем производную n -го порядка или n-ю производную:
.

Производные могут обозначаться штрихами, римскими цифрами, арабскими цифрами в скобках или дробью из дифференциалов. Например, производные третьего и четвертого порядков могут обозначаться так:
;
.

Ниже приведены формулы, которые могут быть полезными при вычислении производных высших порядков.

Полезные формулы производных n-го порядка

Производные некоторых элементарных функций :
;
;
;
;
.

Производная суммы функций :
,
где - постоянные.

Формула Лейбница производной произведения двух функций :
,
где
- биномиальные коэффициенты.

Пример 1

Найти производные первого и второго порядка следующей функции:
.

Находим производную первого порядка. Выносим постоянную за знак производной и применяем формулу из таблицы производных :
.
Применяем правило дифференцирования сложной функции :
.
Здесь .
Применяем правило дифференцирования сложной функции и используем найденные производные:
.
Здесь .

.
Чтобы найти производную второго порядка, нам нужно найти производную от производной первого порядка, то есть от функции:
.
Чтобы не путаться с обозначениями, обозначим эту функцию буквой :
(П1.1) .
Тогда производная второго порядка от исходной функции является производной от функции :
.

Находим производную от функции . Это проще сделать с помощью логарифмической производной . Логарифмируем (П1.1):
.
Теперь дифференцируем:
(П1.2) .
Но - это постоянная. Ее производная равна нулю. Производную от мы уже нашли. Находим остальнве производные по правилу дифференцирования сложной функции.
;
;
.
Подставляем в (П1.2):

.
Отсюда
.

;
.

Пример 2

Найти производную третьего порядка:
.

Находим производную первого порядка . Для этого выносим постоянную за знак производной, используем таблицу производных и применяем правило нахождения производной сложной функции .

.
Здесь .
Итак, мы нашли производную первого порядка:
.

Находим производную второго порядка . Для этого находим производную от . Применяем формулу производной дроби .
.
Производная второго порядка:
.

Теперь находим искомую производную третьего порядка . Для этого дифференцируем .
;
;

.

Производная третьего порядка равна
.

Пример 3

Найти производную шестого порядка следующей функции:
.

Если раскрыть скобки, то будет ясно, что исходная функция является многочленом степени . Запишем ее в виде многочлена:
,
где - постоянные коэффициенты.

Далее применим формулу n-й производной степенной функции:
.
Для производной шестого порядка (n = 6 ) имеем:
.
Отсюда видно, что при . При имеем:
.

Используем формулу производной суммы функций:

.
Таким образом, чтобы найти производную шестого порядка исходной функции, нам надо найти только коэффициент многочлена при старшей степени . Находим его, перемножая старшие степени в произведениях сумм исходной функции:

.
Отсюда . Тогда
.

Пример 4

Найти n-ю производную функции
.

Решение > > >

Пример 5

Найти n-ю производную следующей функции:
,
где и - постоянные.

В этом примере вычисления удобно выполнять с использованием комплексных чисел. Пусть мы имеем некоторую комплексную функцию
(П5.1) ,
где и - функции от действительной переменной x ;
- мнимая единица, .
Дифференцируя (П.1) n раз, имеем:
(П5.2) .
Иногда проще найти n-ю производную от функции . Тогда n-е производные функций и определяются как действительная и мнимая части от n-й производной :
;
.

Применим этот прием для решения нашего примера. Рассмотрим функцию
.
Здесь мы применили формулу Эйлера
,
и ввели обозначение
.
Тогда n-я производная исходной функции определяется по формуле:
.

Найдем n-ю производную функции
.
Для этого применим формулу:
.
В нашем случае
.
Тогда
.

Итак, мы нашли n-ю производную комплексной функции :
,
где .
Найдем действительную часть функции .
Для этого представим комплексное число в показательной форме:
,
где ;
; .
Тогда
;

.

Решение примера
.

Пусть , .
Тогда ;
.
При ,
,
,
.
И мы получаем формулу n-й производной косинуса:
.

,
где
; .

Пусть задана функция двух переменных. Дадим аргументу приращение, а аргумент оставим неизменным. Тогда функция получит приращение, которое называется частным приращением по переменной и обозначается:

Аналогично, фиксируя аргумент и придавая аргументу прираще-ние, получим частное приращение функции по переменной:

Величина называется полным прира-щениием функции в точке.

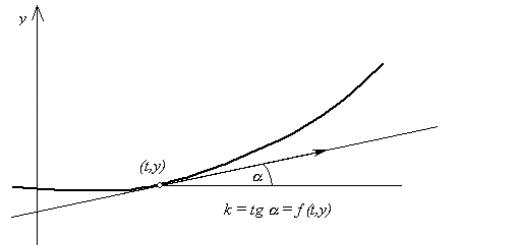
Определение 4. Частной производной функции двух переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению данной переменной, когда последнее стремится к нулю (если этот предел существует). Обозначается частная производная так: или, или.

Таким образом, по определению имеем:

Частные производные функции вычисляются по тем же правилам и формулам, что и функция одной переменной, при этом учитывается, что при дифференцировании по переменной, считается постоянной, а при дифференцировании по переменной постоянной считается.

Пример 3. Найти частные производные функций:

Решение. а) Чтобы найти считаем постоянной величиной и дифференцируем как функцию одной переменной:

Аналогично, считая постоянной величиной, находим:

Определение 5. Полным дифференциалом функции называется сумма произведений частных производных этой функции на приращения соответствующих независимых переменных, т.е.

Учитывая, что дифференциалы независимых переменных совпадают с их приращениями, т.е. , формулу полного дифференциала можно записать в виде

Пример 4. Найти полный дифференциал функции.

Решение. Так как, то по формуле полного дифференциала находим

Частные производные высших порядков

Частные производные и называют частными производными первого порядка или первыми частными производными.

Определение 6. Частными производными второго порядка функции называются частные производные от частных производных первого порядка.

Частных производных второго порядка четыре. Они обозначаются следующим образом:

Аналогично определяются частные производные 3-го, 4-го и более высоких порядков. Например, для функции имеем:

Частные производные второго или более высокого порядка, взятые по различным переменным, называются смешанными частными производными. Для функции таковыми являются производные. Заметим, что в случае, когда смешанные производные непрерывны, то имеет место равенство.

Пример 5. Найти частные производные второго порядка функции

Решение. Частные производные первого порядка для данной функции найдены в примере 3:

Дифференцируя и по переменным х и y, получим

Каждая частная производная (по x и по y ) функции двух переменных представляет собой обыкновенную производную функции одной переменной при фиксированном значении другой переменной:

(где y = const),

(где x = const).

Поэтому частные производные вычисляют по формулам и правилам вычисления производных функций одной переменной , считая при этом другую переменную постоянной (константой).

Если Вам не нужен разбор примеров и необходимого для этого минимума теории, а нужно лишь решение Вашей задачи, то переходите к калькулятору частных производных онлайн .

Если тяжело сосредоточиться, чтобы отслеживать, где в функции константа, то можно в черновом решении примера вместо переменной с фиксированным значением подставить любое число - тогда можно будет быстрее вычислить частную производную как обыкновенную производную функции одной переменной. Надо только не забыть при чистовом оформлении вернуть на место константу (переменную с фиксированном значением).

Описанное выше свойство частных производных следует из определения частной производной, которое может попасться в экзаменационных вопросах. Поэтому для ознакомления с определением ниже можно открыть теоретическую справку.

Понятие непрерывности функции z = f (x , y ) в точке определяется аналогично этому понятию для функции одной переменной.

Функция z = f (x , y ) называется непрерывной в точке если

Разность (2) называется полным приращением функции z (оно получается в результате приращений обоих аргументов).

Пусть заданы функция z = f (x , y ) и точка

Если изменение функции z происходит при изменении только одного из аргументов, например, x , при фиксированном значении другого аргумента y , то функция получит приращение

называемое частным приращением функции f (x , y ) по x .

Рассматривая изменение функции z в зависимости от изменения только одного из аргументов, мы фактически переходим к функции одной переменной.

Если существует конечный предел

то он называется частной производной функции f (x , y ) по аргументу x и обозначается одним из символов

(4)

Аналогично определяются частное приращение z по y :

и частная производная f (x , y ) по y :

(6)

Пример 1.

Решение. Находим частную производную по переменной "икс":

(y фиксировано);

Находим частную производную по переменной "игрек":

(x фиксировано).

Как видно, не имеет значения, в какой степени переменная, которая фиксирована: в данном случае это просто некоторое число, являющееся множителем (как в случае обычной производной) при переменной, по которой находим частную производную. Если же фиксированная переменная не умножена на переменную, по которой находим частную производную, то эта одинокая константа, безразлично, в какой степени, как и в случае обычной производной, обращается в нуль.

Пример 2. Дана функция

Найти частные производные

(по иксу) и (по игреку) и вычислить их значения в точке А (1; 2).

Решение. При фиксированном y производная первого слагаемого находится как производная степенной функции (таблица производных функций одной переменной ):

.

При фиксированном x производная первого слагаемого находится как производная показательной функции, а второго – как производная постоянной:

Теперь вычислим значения этих частных производных в точке А (1; 2):

Проверить решение задач с частными производными можно на калькуляторе частных производных онлайн .

Пример 3. Найти частные производные функции

Решение. В один шаг находим

(y x , как если бы аргументом синуса было 5x : точно так же 5 оказывается перед знаком функции);

(x фиксировано и является в данном случае множителем при y ).

Проверить решение задач с частными производными можно на калькуляторе частных производных онлайн .

Аналогично определяются частные производные функции трёх и более переменных.

Если каждому набору значений (x ; y ; ...; t ) независимых переменных из множества D соответствует одно определённое значение u из множества E , то u называют функцией переменных x , y , ..., t и обозначают u = f (x , y , ..., t ).

Для функций трёх и более переменных геометрической интерпретации не существует.

Частные производные функции нескольких переменных определяются и вычисляются также в предположении, что меняется только одна из независимых переменных, а другие при этом фиксированы.

Пример 4. Найти частные производные функции

.

Решение. y и z фиксированы:

x и z фиксированы:

x и y фиксированы:

Найти частные производные самостоятельно, а затем посмотреть решения

Пример 5.

Пример 6. Найти частные производные функции .

Частная производная функции нескольких переменных имеет тот же механический смысл, что и производная функции одной переменной , - это скорость изменения функции относительно изменения одного из аргументов.

Пример 8. Количественная величина потока П пассажиров железных дорог может быть выражена функцией

где П – количество пассажиров, N – число жителей корреспондирующих пунктов, R – расстоянии между пунктами.

Частная производная функции П по R , равная

показывает, что уменьшение потока пассажиров обратно пропорционально квадрату расстояния между корреспондирующими пунктами при одной и той же численности жителей в пунктах.

Частная производная П по N , равная

показывает, что увеличение потока пассажиров пропорционально удвоенному числу жителей населённых пунктов при одном и том же расстоянии между пунктами.

Проверить решение задач с частными производными можно на калькуляторе частных производных онлайн .

Полный дифференциал

Произведение частной производной на приращение соответствующей независимой переменной называется частным дифференциалом. Частные дифференциалы обозначаются так:

Сумма частных дифференциалов по всем независимым переменным даёт полный дифференциал. Для функции двух независимых переменных полный дифференциал выражается равенством

(7)

Пример 9. Найти полный дифференциал функции

Решение. Результат использования формулы (7):

Функция, имеющая полный дифференциал в каждой точке некоторой области, называется дифференцируемой в этой области.

Найти полный дифференциал самостоятельно, а затем посмотреть решение

Так же как и в случае функции одной переменной, из дифференцируемости функции в некоторой области следует её непрерывность в этой области, но не наоборот.

Сформулируем без доказательств достаточное условие дифференцируемости функции.

Теорема. Если функция z = f (x , y ) имеет непрерывные частные производные

в данной области, то она дифференцируема в этой области и её дифференциал выражается формулой (7).

Можно показать, что подобно тому, как в случае функции одной переменной дифференциал функции является главной линейной частью приращения функции , так и в случае функции нескольких переменных полный дифференциал является главной, линейной относительно приращений независимых переменных частью полного приращения функции.

Для функции двух переменных полное приращение функции имеет вид

(8)

где α и β – бесконечно малые при и .

Частные производные высших порядков

Частные производные и функции f (x , y ) сами являются некоторыми функциями тех же переменных и, в свою очередь, могут иметь производные по разным переменным, которые называются частными производными высших порядков.