Малые свободные колебания механических систем с двумя степенями свободы. Главные колебания. Свободные колебания системы с двумя степенями свободы Линейные колебательные системы с двумя степенями свободы

В частном случае системы с двумя степенями свободы квадратичные формы Т, П, Ф будут соответственно равны

а дифференциальные уравнения малых колебаний примут вид

Рассмотрим свободные колебания консервативной системы. В этом случае

и дифференциальные уравнения принимают вид:

Начальные условия для имеют вид:

В силу положительной определенности квадратичной формы кинетической энергии обобщенные инерционные коэффициенты удовлетворяют соотношениям

а аналогичные соотношения для квазиупругих коэффициентов

являются достаточными условиями устойчивости положения равновесия системы.

Коэффициенты и , связывающие в уравнениях (4.5) обобщенные координаты и , называют соответственно коэффициентами инерционной и упругой связи. Если в колебательной системе коэффициент , ее называют системой с упругой связью, а если – системой с инерционной связью.

Парциальной системой, соответствующей обобщенной координате , называют условную колебательную систему с одной степенью свободы, получаемую из исходной системы, если наложить запрет на изменение всех обобщенных координат, кроме . Парциальными частотами называют собственные частоты парциальных систем:

Поскольку уравнения (4.5) содержат только обобщенные координаты и их вторые производные по времени, ищем их решение в виде

где – пока неопределенные величины.

Подставив (4.8) в (4.5) и приравняв коэффициенты при синусах, получим однородную алгебраическую систему относительно и :

Для того, чтобы однородная алгебраическая система (4.9) имела ненулевое решение, она должна быть вырожденной, т.е. ее определитель должен равняться нулю:

Следовательно, решение (4.7) будет иметь смысл только при тех значениях , которые удовлетворяют условию (4.9). Раскрывая (4.10), получаем

Уравнение, представленное в форме (4.10), (4.11) или (4.12) называют частотным. Как видно из (4.12) частотное уравнение – биквадратное уравнение. Найденные из (4.10)–(4.12) значения называют собственными частотами колебаний системы.

Исследование корней частотного уравнения позволяет сделать следующие выводы:

1) если положение равновесия устойчивое, то оба корня частотного уравнения положительны;

2) первая собственная частота системы всегда меньше меньшей парциальной частоты, а вторая – больше большей парциальной частоты.

Для колебательных систем с упругой связью ( = 0) справедливо равенство

Запишем два частных независимых решения, соответствующих частотам и , в виде

где вторая цифра в индексе соответствует номеру частоты, или номеру тона колебаний.

Константы не являются независимыми, так как система (4.9) вырожденная. Коэффициенты связаны между собой соотношениями

Где . (4.15)

Где . (4.16)

С учетом (4.15) и (4.16) частные решения (4.14) будут иметь вид

Колебания, уравнения которых имеют вид (4.17) называют главными колебаниями. Они представляют собой гармонические колебания с частотами и соответственно. Коэффициенты называют коэффициентами распределения амплитуд. Они характеризуют отношение амплитуд в главных колебаниях или форму главных колебаний.

Коэффициенты распределения амплитуд и, следовательно, формы главных колебаний, как и собственные частоты, определяются параметрами самой колебательной системы и не зависят от начальных условий. Поэтому формы колебаний называют, так же как и частоты, собственными формами колебаний при колебаниях по соответствующему тону.

Общее решение системы уравнений (4.5) может быть представлено как сумма найденных частных решений (4.17)

Общее решение содержит четыре неопределенные постоянные , которые должны определяться из начальных условий (4.6).

При произвольных начальных условиях обе константы и отличны от нуля. Это означает, что изменение во времени каждой обобщенной координаты будет представлять собой сумму гармонических колебаний с частотами и . А такие колебания являются не только не гармоническими, но в общем случае и не периодическими.

Рассмотрим случай свободных колебаний системы, когда собственные частоты колебаний системы и мало отличаются друг от друга:

Обозначим разность аргументов синусов в общем решении (4.18) уравнений свободных колебаний

При величина , а с возрастанием времени эта зависимость из-за малости увеличивается очень медленно. Тогда

С учетом последнего равенства, общее решение уравнений свободных колебаний (4.18) может быть записано в виде:

В этих уравнениях

Так как выражения (4.21) зависят от и , а угол медленно изменяется с изменением времени, то рассматриваемые колебания (4.20) будут колебаниями с периодически изменяющейся амплитудой. Период изменения амплитуды в этом случае значительно больше периода колебаний (рис. 4.1). Если коэффициенты распределения амплитуд и имеют разные знаки, то максимуму соответствует минимум и наоборот. При усилении первого главного колебания интенсивность второго главного колебания уменьшается и наоборот, то есть энергия движения системы периодически оказывается как бы сосредоточенной то в одном, то в другом звене этой вибрирующей системы. Такое явление называют биением.

Возможен другой подход к решению задачи о свободных колебаниях системы – найти какие-то новые обобщенные координаты и называемые нормальными или главными , для которых при любых начальных условиях движение будет одночастотным и гармоническим.

Зависимость между обобщенными координатами и , выбранными произвольно, и главными координатами и можно выразить так:

где и – коэффициенты распределения амплитуд (коэффициенты формы). Можно показать, что переход от исходных координат к главным приводит квадратичные формы кинетической и потенциальной энергии к каноническому виду:

Подставив полученные для и выражения (4.23) в уравнения Лагранжа второго рода, получим уравнения малых колебаний системы в главных координатах: . Выражения кинетической и потенциальной энергии будут иметь канонический вид: и

Как известно, тело, ничем не ограниченное в движениях, называется свободным, так как может двигаться в любом направлении. Отсюда, каждое свободное твердое тело имеет шесть степеней свободы движения. Оно обладает возможностью производить следующие перемещения: три перемещения поступательного характера, соответственно трем основным системам координат, и три вращательных движения вокруг этих трех координатных осей.

Наложение связей (закрепление) уменьшает количество степеней свободы. Так, если тело в одной своей точке закреплено, оно не может производить перемещение вдоль координатных осей, его движения ограничиваются лишь вращением вокруг этих осей, т.е. тело имеет три степени свободы. В том случае, когда закрепленными являются две точки, тело обладает только одной степенью свободы, оно может лишь вращаться вокруг линии (оси), проходящей через обе эти точки. И наконец, при трех закрепленных точках, не лежащих на одной линии, количество степеней свободы равно нулю, и никаких движений тела быть не может. У человека пассивный аппарат движения составляют части его тела, называемые звеньями. Все они соединены между собой, поэтому теряют возможность к трем видам движений вдоль координатных осей. У них остаются только возможности вращения вокруг этих осей. Таким образом, максимальное количество степеней свободы, которым может обладать одно звено тела по отношению к другому звену, смежному с ним, равняется трем.

Это относится к наиболее подвижным суставам человеческого тела, имеющим шаровидную форму.

Последовательно или разветвленные соединения частей тела (звеньев) образуют кинематические цепи.

У человека различают:

- открытые кинематические цепи , имеющие свободный подвижный конец, закрепленный лишь на одном своем конце (например, рука по отношению к туловищу);
- замкнутые кинематические цепи , закрепленные на обоих концах (например, позвонок - ребро - грудина - ребро - позвонок).

Следует отметить, что это касается потенциально возможных размахов движений в суставах. В действительности же у живого человека эти показатели всегда меньше, что доказано многочисленными работами отечественных исследователей - П. Ф. Лесгафтом, М. Ф. Иваницким, М. Г. Привесом, Н. Г. Озолиным и др. На величину подвижности в соединениях костей у живого человека влияет ряд факторов, связанных с возрастом, полом, индивидуальными особенностями, функциональным состоянием нервной системы, степенью растяжения мышц, температурой окружающей среды, временем дня и, наконец, что важно для спортсменов, степенью тренированности. Так, во всех соединениях костей (прерывных и непрерывных) степень подвижности у лиц молодого возраста больше, чем у старшего возраста; у женщин в среднем больше, чем у мужчин. На величину подвижности оказывает влияние степень растяжения тех мышц, которые находятся на стороне, противоположной движению, а также сила мышц, производящих данное движение. Чем эластичнее первые из названных мышц и сильнее вторые, тем размах движений в данном соединении костей больше, и наоборот. Известно, что в холодном помещении движения имеют меньший размах, чем в теплом, утром они меньше, чем вечером. Применение различных упражнений по-разному влияет на подвижность соединений. Так, систематические тренировки упражнениями «на гибкость» увеличивают амплитуду движений в соединениях, тогда как «силовые» упражнения, наоборот, уменьшают ее, приводя, к «закрепощению» суставов. Однако уменьшение амплитуды движений в суставах при применении силовых упражнений не является абсолютно неизбежным. Его можно предотвратить правильным сочетанием силовых упражнений с упражнениями на растяжение тех же самых мышечных групп.

В открытых кинематических цепях человеческого тела подвижность исчисляется десятками степеней свободы. Например, подвижность запястья относительно лопатки и подвижность предплюсны относительно таза насчитывает по семь степеней свободы, а кончики пальцев кисти относительно грудной клетки - 16 степеней свободы. Если суммировать все степени свободы конечностей и головы относительно туловища, то это выразится числом 105, слагающимся из следующих позиций:

- голова - 3 степени свободы;
- руки - 14 степеней свободы;
- ноги - 12 степеней свободы;
- кисти и стопы - 76 степеней свободы.

Для сравнения укажем, что преобладающее большинство машин обладает всего одной степенью свободы движений.

В шаровидных суставах возможны вращения около трех взаимно перпендикулярных осей. Общее же количество осей, около которых возможны в этих суставах вращения, до бесконечности велико. Следовательно, относительно шаровидных суставов можно сказать, что сочленяющиеся в них звенья из возможных шести степеней свободы движений имеют три степени свободы и три степени связанности.

Меньшей подвижностью обладают суставы с двумя степенями свободы движений и четырьмя степенями связанности. К ним относятся суставы яйцевидной или эллипсовидной и седловиной форм, т.е. двухосные. В них возможны движения вокруг этих двух осей.

Одну степень свободы подвижности и вместе с этим пять степеней связанности имеют звенья тела в тех суставах, которые обладают одной осью вращения, т.е. имеют две закрепленные точки.

В преобладающей части суставов тела человека две или три степени свободы. При нескольких степенях свободы движений (двух или более) возможно бесчисленное множество траекторий. Соединения костей черепа имеют шесть степеней связанности и являются неподвижными. Соединение костей при помощи хрящей и связок (синхондрозы и синдесмозы) могут иметь в некоторых случаях значительную подвижность, которая зависит от эластичности и от размеров хрящевых или соединительнотканных образований, находящихся между данными костями.

Рассмотрим малые колебания системы с двумя степенями свободы, на которую действуют силы потенциального поля и силы, периодически меняющиеся по времени. Возникающие при этом движения системы носят название вынужденных колебаний.

Пусть возмущающие обобщенные силы меняются по гармоническому закону от времени, имея равные периоды и начальную фазу. Тогда уравнения движения рассматриваемой системы будут вида:

Уравнения движения в рассматриваемом случае представляют собой систему линейных дифференциальных уравнений второго порядка с постоянными коэффициентами и правой частью.

Переход к главным координатам

Для удобства исследования уравнений движения перейдем в них к главным координатам системы Связь между координатами определяется формулами предыдущего параграфа вида:

Обозначим через соответственно обобщенные силы, соответствующие нормальным координатам Так как обобщенные силы представляют собой коэффициенты при соответствующих вариациях обобщенных координат в выражении элементарной работы действующих на систему сил, то

Следовательно:

Таким образом, уравнения движения в главных координатах приобретают вид:

Уравнения вынужденных колебаний системы с двумя степенями свободы в нормальных координатах независимы друг от друга и могут интегрироваться отдельно.

Критические частоты возмущающей силы

Уравнение для или определяет колебательный характер изменения нормальных координат, подробно изученный при рассмотрении вынужденного колебания точки по прямой, так как дифференциальные уравнения движения в обоих случаях одинаковы. В частности, если частота возмущающей силы равна частоте одного из собственных колебаний системы или то в решение в качестве множителя войдет время t. Следовательно, одна из нормальных обобщенных координат при достаточно большом t будет сколь угодно велика, или мы имеем явление резонанса.

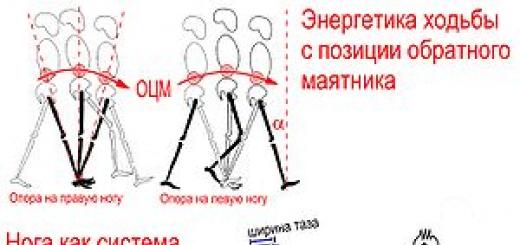
Колебания системы с несколькими степенями свободы, имеющие важные практические приложения, отличаются от колебаний системы с одной степенью свободы рядом существенных особенностей. Чтобы дать представление об этих особенностях, рассмотрим случай свободных колебаний системы с двумя степенями свободы.

Пусть положение системы определяется обобщенными координатами и при система находится в устойчивом равновесии. Тогда кинетическую и потенциальную энергии системы с точностью до квадратов малых величин можно найти так же, как были найдены равенства (132), (133), и представить в виде:

где инерционные коэффициенты и квазиупругие коэффициенты - величины постоянные. Если воспользоваться двумя уравнениями Лагранжа вида (131) и подставить в них эти значения Т и П, то получим следующие дифференциальные уравнения малых колебаний системы с двумя степенями свободы

Будем искать решение уравнений (145) в виде:

где A, B, k, a - постоянные величины. Подставив эти значения в уравнения (145) и сократив на получим

Чтобы уравнения (147) давали для А и В решения, отличные от иуля, определитель этой системы должен быть равен нулю или, иначе, коэффициенты при A и В в уравнениях должны быть пропорциональны, т. е.

Отсюда для определения получаем следующее уравнение, называемое уравнением частот.

Корни этого уравнения вещественны и положительны; это доказывается математически, но может быть обосновано и тем, что иначе не будут вещественны уравнения (145) не будут иметь решений вида (146), чего для системы, находящейся в устойчивом равновесии, быть не может (после возмущений она должна двигаться вблизи положения

Определив нз (149) , найдем две совокупности частных решений вида (146). Если учесть, что согласно эти решения будут:

где и - значения, которые я получает из (148) при и соответственно.

Колебания, определяемые уравнениями (150) и (151), называются главными колебаниями, а их частоты и кг - собственными частотами системы. При этом, колебание с частотой (всегда меныией) называют первым главным колебанием, а с частотой - вторым главным колебанием. Числа определяющие отношения амплитуд (или самих координат, т. е. ) в каждом из этих колебаний, называют коэффициентами формы.

Так как уравнения (145) являются линейными, то суммы частных решений (150) и (151) тоже будут решениями этих уравнений:

Равенства (152), содержащие четыре произвольных постоянных определяемых по начальным условиям, дают общее решение уравнений (145) и определяют закон малых колебаний системы. колебания слагаются из двух главных колебаний с частотами и не являются гармоническими. В частных случаях, при соответствующих начальных условиях, система может совершать одно из главных колебаний (например, первое, если ) и колебание будет гармоническим.

Собственные частоты и коэффициенты формы не зависят от начальных условий и являются основными характеристиками малых колебаний системы; решение конкретных задач обычно сводится к определению этих характеристик.

Сопоставляя результаты этого и предыдущего параграфов, можно получить представление о том, к чему сведется исследование затухающих и вынужденных колебаний системы с двумя степенями свободы. Мы этого рассматривать не будем, отметим лишь, что при вынужденных колебаниях резонанс у такой системы может возникать дважды: при и при ( - частота возмущающей силы). Наконец, отметим, что колебания системы с s степенями свободы будут слагаться из s колебаний с частотами которые должны определяться из уравнения степени s относительно Это связано со значительными математическими трудностями, преодолеть которые можно с помощью электронных вычислительных (или аналоговых) машин.

Задача 185. Определить собственные частоты и коэффициенты формы малых колебаний двойного физического маятника, образованного стержнями и 2 одинаковой массы и длины l (рис. 374, а).

Решение. Выберем в качестве обобщенных координат малые углы . Тогда , где и, при требуемой точности подсчетов, . В итоге

Теория свободных колебаний систем с несколькими степенями свободы строится аналогично тому, как были рассмотрены в § 21 одномерные колебания.

Пусть потенциальная энергия системы U как функция обобщенных координат , имеет минимум при . Вводя малые смещения

и разлагая по ним U с точностью до членов второго порядка, получим потенциальную энергию в виде положительно определенной квадратичной формы

где мы снова отсчитываем потенциальную энергию от ее минимального значения. Поскольку коэффициенты и входят в (23,2) умноженными на одну и ту же величину , то ясно, что их можно всегда считать симметричными по своим индексам

В кинетической же энергии, которая имеет в общем случае вид

(см. (5,5)), полагаем в коэффициентах и, обозначая постоянные посредством , получаем ее в виде положительно определенной квадратичной формы

Таким образом, лагранжева функция системы, совершающей свободные малые колебания:

Составим теперь уравнения движения. Для определения входящих в них производных напишем полный дифференциал функции Лагранжа

Поскольку величина суммы не зависит, разумеется, от обозначения индексов суммирования, меняем в первом и третьем членах в скобках i на k, a k на i; учитывая при этом симметричность коэффициентов , получим:

Отсюда видно, что

Поэтому уравнения Лагранжа

(23,5)

Они представляют собой систему линейных однородных дифференциальных уравнений с постоянными коэффициентами.

По общим правилам решения таких уравнений ищем s неизвестных функций в виде

где - некоторые, пока неопределенные, постоянные. Подставляя (23,6) в систему (23,5), получаем по сокращении на систему линейных однородных алгебраических уравнений, которым должны удовлетворять постоянные :

Для того чтобы эта система имела отличные от нуля решения, должен обращаться в нуль ее определитель

Уравнение (23.8) - так называемое характеристическое уравнение представляет собой уравнение степени s относительно Оно имеет в общем случае s различных вещественных положительных корней (в частных случаях некоторые из этих корней могут совпадать). Определенные таким образом величины называются собственными частотами системы.

Вещественность и положительность корней уравнения (23,8) заранее очевидны уже из физических соображений. Действительно, наличие у со мнимой части означало бы наличие во временной зависимости координат (23,6) (а с ними и скоростей ) экспоненциально убывающего или экспоненциально возрастающего множителя. Но наличие такого множителя в данном случае недопустимо, так как оно привело бы к изменению со временем полной энергии системы в противоречии с законом ее сохранения.

В том же самом можно убедиться и чисто математическим путем. Умножив уравнение (23,7) на и просуммировав затем по получим:

Квадратичные формы в числителе и знаменателе этого выражения вещественны в силу вещественности и симметричности коэффициентов и , действительно,

Они также существенно положительны, а потому положительно

После того как частоты найдены, подставляя каждое из них в уравнения (23,7), можно найти соответствующие значения коэффициентов Если все корни характеристического уравнения различны, то, как известно, коэффициенты А пропорциональны минорам определителя (23,8), в котором и заменена соответствующим значением обозначим эти миноры через До. Частное решение системы дифференциальных уравнений (23,5) имеет, следовательно, вид

где - произвольная (комплексная) постоянная.

Общее же решение даетбя суммой всех s частных решений. Переходя к вещественной части, напишем его в виде

где мы ввели обозначение

(23,10)

Таким образом, изменение каждой из координат системы со временем представляет собрй наложение s простых периодических колебаний с произвольными амплитудами и фазами, но имеющих вполне определенные частоты.

Естественно возникает вопрос, нельзя ли выбрать обобщенные координаты таким образом, чтобы каждая из них совершала только одно простое колебание? Самая форма общего интеграла (23,9) указывает путь к решению этой задачи.

В самом деле, рассматривая s соотношений (23,9) как систему уравнений с s неизвестными величинами мы можем, разрешив эту систему, выразить величины через координаты . Следовательно, величины можно рассматривать как новые обобщенные координаты. Эти координаты называют нормальными (или главными), а совершаемые ими простые периодические колебания - нормальными колебаниями системы.

Нормальные координаты удовлетворяют, как это явствует из их определения, уравнениям

(23,11)

Это значит, что в нормальных координатах уравнения движения распадаются на s независимых друг от друга уравнений. Ускорение каждой нормальной координаты зависит только от значения этой же координаты, и для полного определения ее временной зависимости надо знать начальные значения только ее же самой и соответствующей ей скорости. Другими словами, нормальные колебания системы полностью независимы.

Из сказанного очевидно, что функция Лагранжа, выраженная через нормальные координаты, распадается на сумму выражений, каждое из которых соответствует одномерному колебанию с одной из частот т. е. имеет вид

(23,12)

где - положительные постоянные. С математической точки зрения это означает, что преобразованием (23,9) обе квадратичные формы - кинетическая энергия (23,3) и потенциальная (23,2) одновременно приводятся к диагональному виду.

Обычно нормальные координаты выбирают таким образом, чтобы коэффициенты при квадратах скоростей в функции Лагранжа были равны 1/2. Для этого достаточно определить нормальные координаты (обозначим их теперь ) равенствами

Все изложенное мало меняется в случае, когда среди корней характеристического уравнения имеются кратные корни. Общий вид (23,9), (23,10) интеграла уравнений движений остается таким же (с тем же числом s членов) с той лишь разницей, что соответствующие кратным частотам коэффициенты уже не являются минорами определителя, которые, как известно, обращаются в этом случае в нуль.

Каждой кратной (или, как говорят, вырожденной) частоте отвечает столько различных нормальных координат, какова степень кратности, но выбор этих нормальных координат не однозначен. Поскольку в кинетическую и потенциальную энергии нормальные координаты (с одинаковым ) входят в виде одинаково преобразующихся сумм то их можно подвергнуть любому линейному преобразованию, оставляющему инвариантной сумму квадратов.

Весьма просто нахождение нормальных координат для трехмерных колебаний одной материальной точки, находящейся в постоянном внешнем поле. Помещая начало декартовой системы координат в точку минимума потенциальной энергии мы получим последнюю в виде квадратичной формы переменных х, у, z, а кинетическая энергия

(m - масса частиц) не зависит от выбора направления координатных осей. Поэтому соответствующим поворотом осей надо только привести к диагональному виду потенциальную энергию. Тогда

и колебания вдоль осей х, у, z являются главными с частотами

В частном случае центрально-симметричного поля эти три частоты совпадают (см. задачу 3).

Использование нормальных координат дает возможность привести задачу о вынужденных колебаниях системы с несколькими степенями свободы к задачам об одномерных вынужденных колебаниях. Функция Лагранжа системы с учетом действующих на нее переменных внешних сил имеет вид

(23,15)