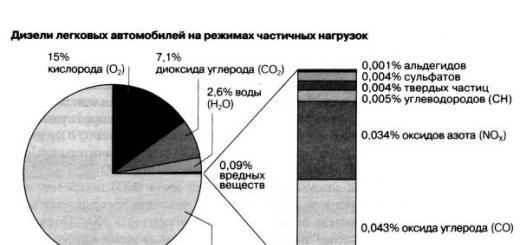
Предел и непрерывность

функции одной переменной

3.1.1. Определение. Число А x стремящимся к x 0 , если для любого числа
найдётся число
(
), и будет выполняться условие:

если
, то
.

(Символика:
).

Если точки графика Г функции

, когда неограниченно близко приближается к точке (т.е.
), (см. Рис. 3.1), то это обстоятельство является геометрическим эквивалентом того, что функция
при
имеет предельное значение (предел) A (символика:
).

График функции ,

Рис. 3.1

Следует отметить, что в определении предельного значения (предела) функции при x стремящемся к x 0 ничего не говорится о поведении функции в точке x 0 . В самой точке x 0 функция может быть не определена, может быть
, а может быть
.

Если
, то функция называется бесконечно малой при
.

Промежуток называют  - окрестностью точки x 0 с выколотым центром. Используя это название, можно сказать так: , если для любого числа найдётся число , и будет выполняться условие: если
, то
.

3.1.2. Определение. , если для любой сходящейся к x 0 последовательности
последовательность
сходится к А .

3.1.3. Докажем эквивалентность определений разделов 3.1.1 и 3.1.2

Пусть сначала в смысле первого определения и пусть
(
), тогда все , кроме их конечного числа удовлетворяют неравенству
, где  выбрано по  в смысле первого определения, т.е.
, т.е. из первого определения следует второе. Пусть теперь
в смысле второго определения и допустим, что в смысле второго определения
, т.е. для некоторого при сколь угодно малых (например, при
) нашлась последовательность
, но при этом
. Пришли к противоречию, следовательно, из второго определения следует первое.

3.1.4. Эквивалентность этих определений особенно удобна, ибо все доказанные ранее теоремы о свойствах пределов для последовательностей переносятся почти автоматически на новый случай. Следует лишь уточнить понятие ограниченности. Соответствующая теорема имеет следующую формулировку:

Если
, то ограничена на некоторой  - окрестности точки x 0 с выколотым центром.

3.2.1.Теорема. Пусть
,
,

тогда,
,

,

.

3.2.2. Пусть

- произвольная, сходящаяся к x 0 последовательность значений аргументов функций и
. Соответствующие последовательности
и
значений этих функций имеют пределы A и B . Но тогда, в силу теоремы раздела 2.13.2, последовательности
,
и
имеют пределы, соответственно равные A +B ,
и
. Согласно определению предела функции в точке (см. раздел 2.5.2) это означает, что

,
,

.

3.2.3. Теорема. Если
,
, и в некоторой окрестности

имеет место

.

3.2.4. По определению предела функции в точке x 0 для любой последовательности
такой, что

последовательность значений функции имеет предел равный А . Это означает, что для любого
существует номер
выполняется . Аналогично, для последовательности
существует номер
такой, что для любого номера
выполняется . Выбирая
, получаем, что для всех
выполняется . Из этой цепочки неравенств имеем для любого , что означает, что
.

3.2.5. Определение. Число А называется предельным значением (пределом) функции при x стремящимся к x 0 справа (символика:
), если для любого числа найдётся число () и будет выполняться условие: если
, то
.

Множество называют правой  - окрестностью точки x 0 . Аналогично определяется понятие предельного значения (предела) слева (
).

3.2.6. Теорема. Функция при имеет предельное значение (предел) равный А тогда и только тогда, когда

,

3.3.1. Определение. Число А называется предельным значением (пределом) функции при x стремящимся к бесконечности, если для любого числа найдётся число
(
) и будет выполняться условие:

если
, то .

(Символика:
.)

Множество
называется D -окрестностью бесконечности.

3.3.2. Определение. Число А называется предельным значением (пределом) функции при x стремящимся к плюс бесконечности, если для любого числа найдётся число D () и будет выполняться условие:

если
, то .

(Символика:
).

Если точки графика Г функции
с неограниченным ростом
неограниченно приближаются к единственной горизонтальной прямой
(см. Рис. 3.2), то это обстоятельство является геометрическим эквивалентом того, что функция
при
имеет предельное значение (предел), равное числу A (символика:
).

График функции
,

Множество
называется D -окрестностью плюс бесконечности.

Аналогично определяется понятие предела при
.

Упражнения.

Сформулируйте все теоремы о пределах применительно к случаям:

1)
, 2)
, 3)
, 4)
, 5)
.

3.4.1. Определение. Функция называется бесконечно большой функцией (или просто бесконечно большой) при , если для любого числа

, удовлетворяющих неравенству , выполняется неравенство
.

(Символика:
.)

Если выполняется
, то пишут
.

Если выполняется
, то пишут
.

3.4.2. Теорема. Пусть
и
при
.

Тогда
- бесконечно большая функция при .

3.4.3. Пусть произвольное число . Так как - бесконечно малая функция при , то для числа
существует число такое, что для всех x таких, что выполняется неравенство
, но тогда для тех же x выполнятся неравенство
. Т.е. - бесконечно большая функция при .

3.4.4.Теорема. Пусть - бесконечно большая функция при и при .

Тогда - бесконечно малая функция при .

(Эта теорема доказывается аналогично теореме раздела 3.8.2).

3.4.5. Функция
называется неограниченной при
, если для любого числа
и любой δ-окрестности точки можно указать точку x из этой окрестности такую, что
.

3.5.1. ОПРЕДЕЛЕНИЕ. Функция называется непрерывной в точке , если
.

Последнее условие можно записать и так:

.

Эта запись означает, что для непрерывных функций можно менять местами знак предела и знак функции

Или так: . Или снова, как в начале.

Обозначим
. Тогда
и =
и последняя форма записи примет вид

.

Выражение под знаком предела представляет собой приращение функции точке , вызванное приращением
аргумента x в точке , обозначаемое обычно как
. В итоге получаем следующую форму записи условия непрерывности функции в точке

,

которую называют «рабочим определением» непрерывности функции в точке.

Функция называется непрерывной в точке слева , если
.

Функция называется непрерывной в точке справа , если
.

3.5.2. Пример.
. Эта функция непрерывна для любого . С помощью теорем о свойствах пределов, мы сразу получаем: любая рациональная функция непрерывна в каждой точке, в которой она определена, т.е. функция вида
.

УПРАЖНЕНИЯ .

3.6.1. В школьном учебнике доказывается (на высоком уровне строгости), что
(первый замечательный предел). Из наглядных геометрических соображений сразу получается, что
. Заметим, что из левого неравенства следует также, что
, т.е. что функция
непрерывна в нуле. Отсюда уж совсем нетрудно доказать непрерывность всех тригонометрических функций во всех точках, где они определены. В самом деле, при
как произведение бесконечно малой функции
на ограниченную функцию
.

3.6.2. (2-й замечательный предел). Как нам уже известно

,

где пробегает натуральные числа. Можно показать, что
. Более того
.

УПРАЖНЕНИЯ .

3.7.1. ТЕОРЕМА (о непрерывности сложной функции).

Если функция
непрерывна в точке и
, а функция
непрерывна в точке , то сложная функция
непрерывна в точке .

3.7.2. Справедливость этого утверждения немедленно следует из определения непрерывности, записанного в виде:

3.8.1. ТЕОРЕМА. Функция непрерывна в каждой точке (
).

3.8.2. Если считать обоснованным, что функция
определена для любого и является строго монотонной (строго убывающей при
, строго возрастающей при
), то доказательство не составляет труда.

При
имеем:

т.е. при имеем
, что означает, что функция непрерывна при .

При
всё сводится к предыдущему:

При
.

При
функция
постоянна при всех , следовательно, непрерывна.

3.9.1. ТЕОРЕМА (о сосуществовании и непрерывности обратной функции).

Пусть непрерывная функция строго убывает (строго возрастает) в некоторой δ - окрестности точки ,
. Тогда в некоторой ε - окрестности точки существует обратная функция
, которая строго убывает (строго возрастает) и непрерывна в ε - окрестности точки .

3.9.2. Докажем здесь только непрерывность обратной функции в точке .

Возьмём , точка y расположена между точками
и
, следовательно, если
, то
, где .

3.10.1. Итак, любые позволительные арифметические действия над непрерывными функциями вновь приводят к непрерывным функциям. Образование из них сложных и обратных функций не портит непрерывности. Поэтому, с некоторой долей ответственности, мы можем утверждать, что все элементарные функции при всех допустимых значениях аргумента непрерывны.

УПРАЖНЕНИЕ .

Докажите, что
при
(другая форма второго замечательного предела).

3.11.1. Вычисление пределов сильно упрощается, если использовать понятие эквивалентных бесконечно малых. Понятие эквивалентности удобно обобщить на случай произвольных функций.

Определение. Функции и называются эквивалентными при , если
(вместо можно писать
,
,
,
,
).

Используемое обозначение f ~ g .

Эквивалентность обладает следующими свойствами

Необходимо помнить следующий список эквивалентных бесконечно малых:

~
при
; (1)

~ при ; (2)

~
при ; (3)

~ при ; (4)

~ при ; (5)

~ при ; (6)

~ при ; (7)

~ p при ; (8)

~ при
; (9)

~
при . (10)

Здесь и могут быть не независимыми переменными, а функциями
и
стремящимися соответственно к нулю и единице при некотором поведении x . Так, например,

~
при
,

~
при
.

Эквивалентность (1) является иной формой записи первого замечательного предела. Эквивалентности (2), (3), (6) и (7) можно доказать непосредственно. Эквивалентность (4) получается из (1) с учётом свойства 2) эквивалентностей:

~
.

Аналогично (5) и (7) получаются из (2) и (6). В самом деле

~
,

~
.

Эквивалентность (8) доказывается последовательным применением (7) и (6):

а (9) и (10) получаются из (6) и (8) заменой
.

3.11.2. Теорема. При вычислении пределов в произведении и отношении можно менять функции на эквивалентные. А именно, если ~
, то, либо оба предела не существуют одновременно, и
, либо оба эти предела не существуют одновременно.

Докажем первое равенство. Пусть один из пределов, скажем,
существует. Тогда

.

3.11.3. Пусть (- число или символ ,
или
). Будем рассматривать поведение различных б.м. функций (так будем сокращать термин бесконечно малая).

ОПРЕДЕЛЕНИЯ.
и называются эквивалентными б.м. функциями при , если
(при ).

будем называть б.м. более высокого порядка чем б.м. функция
, если
(при ).

3.11.4. Если и эквивалентные б.м. функции, то
есть б.м. функция более высокого порядка чем
и чем . - б.м. функции при, в которой для всех x и, если в этой точке функция называется точкой устранимого разрыва. имеет разрыв второго рода. Сама точкаКонтрольная работа

К коллоквиуму. Разделы: «Предел и непрерывность функции действительной переменной» функции одной переменной» , «Дифференциальное исчисление функций нескольких переменных»

Тематика и примеры контрольных заданий и вопросов (контрольные работы индивидуальные типовые расчеты коллоквиум) i семестр контрольная работа №1 раздел «предел и непрерывность функции действительной переменной»

Контрольная работа

К коллоквиуму. Разделы: «Предел и непрерывность функции действительной переменной» , «Дифференциальное исчисление функции одной переменной» , «Дифференциальное исчисление функций нескольких переменных» . Числовая последовательность...

Контрольная работа

К коллоквиуму. Разделы: «Предел и непрерывность функции действительной переменной» , «Дифференциальное исчисление функции одной переменной» , «Дифференциальное исчисление функций нескольких переменных» . Числовая последовательность...

Тематика и примеры контрольных заданий и вопросов (контрольная работа индивидуальные типовые расчеты коллоквиумы) i семестр контрольная работа раздел «предел и непрерывность функции действительной переменной»

Контрольная работа

К коллоквиуму. Разделы: «Предел и непрерывность функции действительной переменной» , «Дифференциальное исчисление функции одной переменной» , «Дифференциальное исчисление функций нескольких переменных» . Числовая последовательность...

Лекция 19 предел и непрерывность функции нескольких переменных

Лекция

... Предел и непрерывность функции нескольких переменных . 19.1. Понятие функции нескольких переменных . При рассмотрении функций нескольких переменных ... свойствам функций одной переменной , непрерывных на отрезке. См. Свойства функций , непрерывных на...

Понятие предела числовой последовательности

Вспомним сначала определение числовой последовательности.

Определение 1

Отображения множества натуральных чисел на множество действительных чисел называется числовой последовательностью .

Понятие предела числовой последовательности имеет несколько основных определений:

• Действительное число $a$ называется пределом числовой последовательности $(x_n)$, если для любого $\varepsilon >0$ существует номер $N$, зависящий от $\varepsilon$, такой, что для любого номера $n> N$ выполняется неравенство $\left|x_n-a\right|
• Действительное число $a$ называется пределом числовой последовательности $(x_n)$, если в любую окрестность точки $a$ попадают все члены последовательности $(x_n)$, за исключением, быть может, конечного числа членов.

Рассмотрим пример вычисления значения предела числовой последовательности:

Пример 1

Найти предел ${\mathop{lim}_{n\to \infty } \frac{n^2-3n+2}{2n^2-n-1}\ }$

Решение:

Для решения данного задания вначале нам необходимо вынести за скобки старшую степень, входящую в выражение:

${\mathop{lim}_{n\to \infty } \frac{n^2-3n+2}{2n^2-n-1}\ }={\mathop{lim}_{x\to \infty } \frac{n^2\left(1-\frac{3}{n}+\frac{2}{n^2}\right)}{n^2\left(2-\frac{1}{n}-\frac{1}{n^2}\right)}\ }={\mathop{lim}_{n\to \infty } \frac{1-\frac{3}{n}+\frac{2}{n^2}}{2-\frac{1}{n}-\frac{1}{n^2}}\ }$

Если в знаменателе стоит бесконечно большая величина, то весь предел стремится к нулю, $\mathop{lim}_{n\to \infty }\frac{1}{n}=0$, использовав это, получим:

${\mathop{lim}_{n\to \infty } \frac{1-\frac{3}{n}+\frac{2}{n^2}}{2-\frac{1}{n}-\frac{1}{n^2}}\ }=\frac{1-0+0}{2-0-0}=\frac{1}{2}$

Ответ: $\frac{1}{2}$.

Понятие предела функции в точке

Понятие предела функции в точке имеет два классических определения:

Определение термина «предел» по Коши

Действительное число $A$ называется пределом функции $f\left(x\right)$ при $x\to a$, если для любого $\varepsilon > 0$ существует $\delta >0$, зависящий от $\varepsilon $, такой, что для любого $x\in X^{\backslash a}$, удовлетворяющих неравенству $\left|x-a\right|

Определение по Гейне

Действительное число $A$ называется пределом функции $f\left(x\right)$ при $x\to a$, если для любой последовательности $(x_n)\in X$, сходящейся к числу $a$, последовательность значений $f(x_n)$ сходится к числу $A$.

Эти два определения связаны между собой.

Замечание 1

Определения предела функции по Коши и по Гейне эквивалентны.

Помимо классических подходов к вычислению пределов функции, вспомним формулы, которые могут также помочь в этом.

Таблица эквивалентных функций, когда $x$ бесконечно мал (стремится к нулю)

Одним из подходов к решению пределов является принцип замены на эквивалентную функцию . Таблица эквивалентных функций представлена ниже, чтобы ей воспользоваться, необходимо вместо функций справа подставить в выражение соответствующую элементарную функцию слева.

Рисунок 1. Таблица эквивалентности функций. Автор24 - интернет-биржа студенческих работ

Также для решения пределов, значения которых сводятся к неопределённости, возможно применить правило Лопиталя. В общем случае неопределённость вида $\frac{0}{0}$ можно раскрыть разложив на множители числитель и знаменатель и затем сократив. Неопределённость, имеющую форму $\frac{\infty }{\infty}$ возможно разрешить после деления выражений в числителе и знаментателе на переменную, при которой находится старшая степень.

Замечательные пределы

• Первый замечательный предел:

${\mathop{lim}_{x\to 0} \frac{sinx}{x}\ }=1$

• Второй замечательный предел:

$\mathop{lim}_{x\to 0}{(1+x)}^{\frac{1}{x}}=e$

Специальные пределы

• Первый специальный предел:

$\mathop{lim}_{x\to 0}\frac{{{log}_a (1+x-)\ }}{x}={{log}_a e\ }=\frac{1}{lna}$

• Второй специальный предел:

$\mathop{lim}_{x\to 0}\frac{a^x-1}{x}=lna$

• Третий специальный предел:

$\mathop{lim}_{x\to 0}\frac{{(1+x)}^{\mu }-1}{x}=\mu $

Непрерывность функции

Определение 2

Функция $f(x)$ называется непрерывной в точке $x=x_0$, если $\forall \varepsilon >{\rm 0}$ $\exists \delta (\varepsilon ,E_{0})>{\rm 0}$ такое, что $\left|f(x)-f(x_{0})\right|

Функция $f(x)$ непрерывна в точке $х=х_0$, если $\mathop{{\rm lim\; }}\limits_{{\rm x}\to {\rm x}_{{\rm 0}} } f(x)=f(x_{0})$.

Точка $x_0\in X$ называется точкой разрыва первого рода, если в ней существуют конечные пределы ${\mathop{lim}_{x\to x_0-0} f(x_0)\ }$, ${\mathop{lim}_{x\to x_0+0} f(x_0)\ }$, но нарушается равенство ${\mathop{lim}_{x\to x_0-0} f(x_0)\ }={\mathop{lim}_{x\to x_0+0} f(x_0)\ }=f(x_0)$

Причем, если ${\mathop{lim}_{x\to x_0-0} f(x_0)\ }={\mathop{lim}_{x\to x_0+0} f(x_0)\ }\ne f(x_0)$, то это точка устранимого разрыва, а если ${\mathop{lim}_{x\to x_0-0} f(x_0)\ }\ne {\mathop{lim}_{x\to x_0+0} f(x_0)\ }$, то точка скачка функции.

Точка $x_0\in X$ называется точкой разрыва второго рода, если в ней хотя бы один из пределов ${\mathop{lim}_{x\to x_0-0} f(x_0)\ }$, ${\mathop{lim}_{x\to x_0+0} f(x_0)\ }$ представляет собой бесконечность или не существует.

Пример 2

Исследовать на непрерывность $y=\frac{2}{x}$

Решение:

${\mathop{lim}_{x\to 0-0} f(x)\ }={\mathop{lim}_{x\to 0-0} \frac{2}{x}\ }=-\infty $ - функция имеет точку разрыва второго рода.

ПЕРЕМЕННЫЕ И ПОСТОЯННЫЕ ВЕЛИЧИНЫ

В результате измерения физических величин (время, площадь, объем, масса, скорость и т.д.) определяются их числовые значения. Математика занимается величинами, отвлекаясь от их конкретного содержания. В дальнейшем, говоря о величинах, мы будем иметь в виду их числовые значения. В различных явлениях некоторые величины изменяются, а другие сохраняют свое числовое значение. Например, при равномерном движении точки время и расстояние меняются, а скорость остается постоянной.

Переменной величиной называется величина, которая принимает различные числовые значения. Величина, числовые значения которой не меняются, называется постоянной . Переменные величины будем обозначать буквами x, y, z,… , постоянные – a, b, c,…

Заметим, что в математике постоянная величина часто рассматривается как частный случай переменной, у которой все числовые значения одинаковы.

Областью изменения переменной величины называется совокупность всех принимаемых ею числовых значений. Область изменения может состоять как из одного или нескольких промежутков, так и из одной точки.

УПОРЯДОЧЕННАЯ ПЕРЕМЕННАЯ ВЕЛИЧИНА. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ

Будем говорить, что переменная x есть упорядоченная переменная величина , если известна область ее изменения, и про каждые из двух любых ее значений можно сказать, какое из них предыдущее и какое последующее.

Частным случаем упорядоченной переменной величины является переменная величина, значения которой образуют числовую последовательность x 1 ,x 2 ,…,x n ,… Для таких величин при i < j, i, j Î N , значение x i считается предшествующим, а x j – последующим независимо от того, какое из этих значений больше. Таким образом, числовая последовательность – это переменная величина, последовательные значения которой могут быть перенумерованы. Числовую последовательность будем обозначать . Отдельные числа последовательности называются ее элементами .

Например, числовую последовательность образуют следующие величины:

ФУНКЦИЯ

При изучении различных явлений природы и решении технических задач, а, следовательно, и в математике приходится рассматривать изменение одной величины в зависимости от изменения другой. Так, например, известно, что площадь круга выражается через радиус формулой S = πr 2 . Если радиус r принимает различные числовые значения, то площадь S также принимает различные числовые значения, т.е. изменение одной переменной влечет изменение другой.

Если каждому значению переменной x , принадлежащему некоторой области, соответствует одно определенное значение другой переменной y , то y называется функцией переменной х . Символически будем записывать y=f(x) . При этом переменная x называется независимой переменной или аргументом .

Запись y=C , где C – постоянная, обозначает функцию, значение которой при любом значении x одно и то же и равно C .

Множество значений x , для которых можно определить значения функции y по правилу f(x) , называется областью определения функции .

Заметим, что числовая последовательность также является функцией, область определения которой совпадает с множеством натуральных чисел.

К основным элементарным функциям относятся все функции, изучаемые в школьном курсе математики:

Элементарной функцией называется функция, которая может быть задана основными элементарными функциями и постоянными при помощи конечного числа операций сложения, вычитания, умножения, деления и взятия функции от функции.

ПОНЯТИЕ ПРЕДЕЛА ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ

В дальнейшем курсе математики понятие предела будет играть фундаментальную роль, так как с ним непосредственно связаны основные понятия математического анализа – производная, интеграл и др.

Начнем с понятия предела числовой последовательности.

Число a называется пределом последовательности x = {x n }, если для произвольного заранее заданного сколь угодно малого положительного числа ε найдется такое натуральное число N , что при всех n>N выполняется неравенство |x n - a| < ε.

Если число a есть предел последовательности x = {x n }, то говорят, что x n стремится к a , и пишут .

Чтобы сформулировать это определение в геометрических терминах введем следующее понятие.

Окрестностью точки x 0 называется произвольный интервал (a, b ), содержащий эту точку внутри себя. Часто рассматривается окрестность точки x 0 , для которой x 0 является серединой, тогда x 0 называется центром окрестности, а величина (b –a )/2 – радиусом окрестности.

Итак, выясним, что же означает геометрически понятие предела числовой последовательности. Для этого запишем последнее неравенство из определения в виде

Это неравенство означает, что все элементы последовательности с номерами n>N должны лежать в интервале (a – ε; a + ε).

Следовательно, постоянное число a есть предел числовой последовательности {x n }, если для любой малой окрестности с центром в точке a радиуса ε (ε – окрестности точки a ) найдется такой элемент последовательности с номером N , что все последующие элементыс номерами n>N будут находиться внутри этой окрестности.

Примеры.

Сделаем несколько замечаний.

Замечание 1. Очевидно, что если все элементы числовой последовательности принимают одно и то же постоянное значение x n = c , то предел этой последовательности будет равен самой постоянной. Действительно, при любом ε всегда выполняется неравенство |x n - c | = |c - c | = 0 < ε.

Замечание 2. Из определения предела следует, что последовательность не может иметь двух пределов. Действительно, предположим, что x n → a и одновременно x n → b . Возьмем любое и отметим окрестности точек a и b радиуса ε (см. рис.). Тогда по определению предела, все элементы последовательности, начиная с некоторого, должны находиться как в окрестности точки а , так и в окрестности точки b , что невозможно.

Замечание 3. Не следует думать, что каждая числовая последовательность имеет предел. Пусть, например, переменная величина принимает значения . Несложно заметить, что эта последовательность не стремится ни к какому пределу.

ПРЕДЕЛ ФУНКЦИИ

Пусть функция y=f(x) определена в некоторой окрестности точки a . Предположим, что независимая переменная x неограниченно приближается к числу a . Это означает, что мы можем придавать х значения сколь угодно близкие к a , но не равные a . Будем обозначать это так x → a . Для таких x найдем соответствующие значения функции. Может случиться, что значения f(x) также неограниченно приближаются к некоторому числу b .Тогда говорят, что число b есть предел функции f(x) при x → a .

Введем строгое определение предела функции.

Функция y=f(x) стремится к пределу b при x → a , если для каждого положительного числа ε, как бы мало оно не было, можно указать такое положительное число δ, что при всех x ≠ a из области определения функции, удовлетворяющих неравенству |x - a | < δ, имеет место неравенство |f(x) - b | < ε. Если b есть предел функции f(x) при x → a , то пишут или f(x) → b при x → a .

Проиллюстрируем это определение на графике функции. Т.к. из неравенства |x - a | < δ должно следовать неравенство |f(x) - b | < ε, т.е. при x Î (a - δ, a + δ) соответствующие значения функции f(x) Î (b - ε, b + ε), то, взяв произвольное ε > 0, мы можем подобрать такое число δ, что для всех точек x , лежащих в δ – окрестности точки a , соответствующие точки графика функции должны лежать внутри полосы шириной 2ε, ограниченной прямыми y = b – ε и y = b + ε.

Несложно заметить, что предел функции должен обладать теми же свойствами, что и предел числовой последовательности, а именно и если при x → a функция имеет предел, то он единственный.

Примеры.

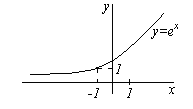
ПОНЯТИЕ ПРЕДЕЛА ФУНКЦИИ В БЕСКОНЕЧНО УДАЛЕННОЙ ТОЧКЕ

До сих пор мы рассматривали пределы для случая, когда переменная величина x стремилась к определенному постоянному числу.

Будем говорить, что переменная x стремится к бесконечности , если для каждого заранее заданного положительного числа M (оно может быть сколь угодно большим) можно указать такое значение х=х 0 , начиная с которого, все последующие значения переменной будут удовлетворять неравенству |x|>M .

Например, пусть переменная х принимает значения x 1 = –1, x 2 = 2, x 3 = –3, …, x n =(–1) n n, … Ясно, что это бесконечно большая переменная величина, так как при всех M > 0 все значения переменной, начиная с некоторого, по абсолютной величине будут больше M .

Переменная величина x → +∞ , если при произвольном M > 0 все последующие значения переменной, начиная с некоторого, удовлетворяют неравенству x > M .

Аналогично, x → – ∞, если при любом M > 0 x < -M .

Будем говорить, что функция f(x) стремится к пределу b при x → ∞, если для произвольного малого положительного числа ε можно указать такое положительное число M , что для всех значений x , удовлетворяющих неравенству |x|>M , выполняется неравенство |f(x) - b | < ε.

Обозначают .

Примеры.

БЕСКОНЕЧНО БОЛЬШИЕ ФУНКЦИИ

Ранее мы рассмотрели случаи, когда функция f(x) стремилась к некоторому конечному пределу b при x → a или x → ∞.

Рассмотрим теперь случай, когда функция y=f(x) некотором способе изменения аргумента.

Функция f(x) стремится к бесконечности при x → a , т.е. является бесконечно большой величиной, если для любого числа М , как бы велико оно ни было, можно найти такое δ > 0, что для всех значений х ≠a , удовлетворяющих условию |x-a | < δ, имеет место неравенство |f(x) | > M .

Если f(x) стремится к бесконечности при x→a , то пишут или f(x) →∞ при x→a .

Сформулируйте аналогичное определение для случая, когда x →∞.

Если f(x) стремится к бесконечности при x→a и при этом принимает только положительные или только отрицательные значения, соответственно пишут или .

Примеры.

ОГРАНИЧЕННЫЕ ФУНКЦИИ

Пусть задана функция y=f(x) , определенная на некотором множестве D значений аргумента.

Функция y=f(x) называется ограниченной на множестве D , если существует положительное число М такое, что для всех значений x из рассматриваемого множества, выполняется неравенство |f(x)|≤M . Если же такого числа М не существует, то функция f(x) называется неограниченной на множестве D .

Примеры.

1. Функция y =sin x , определенная при -∞<x <+∞, является ограниченной, так как при всех значениях x |sin x |≤1 = M .
2. Функция y =x 2 +2 ограничена, например, на отрезке , так как при всех x из этого отрезка |f(x)| ≤f (3) = 11.
3. Рассмотрим функцию y =ln x при x Î (0; 1). Эта функция неограниченна на указанном отрезке, так как при x →0 ln x →-∞.

Функция y=f(x) называется ограниченной при x → a , если существует окрестность с центром в точке а , в которой функция ограничена.

Функция y=f(x) называется ограниченной при x→∞ , если найдется такое число N> 0, что при всех значениях х |x|>N , функция f(x) ограничена.

Установим связь между ограниченной функцией и функцией, имеющей предел.

Теорема 1. Если и b – конечное число, то функция f(x) ограничена при x→a .

Доказательство . Т.к. , то при любом ε>0 найдется такое число δ>0, что при вех значениях х , удовлетворяющих неравенству |x-a|< δ, выполняется неравенство |f(x) –b|< ε. Воспользовавшись свойством модуля |f(x) – b|≥|f(x)| - |b| , последнее неравенство запишем в виде |f(x)|<|b|+ ε. Таким образом, если положить M=|b|+ ε, то при x→a |f(x)|

Замечание. Из определения ограниченной функции следует, что если , то она является неограниченной. Однако обратное неверно: неограниченная функция может не быть бесконечно большой. Приведите пример.

Теорема 2. Если , то функция y=1/f(x) ограничена при x→a .

Доказательство . Из условия теоремы следует, что при произвольном ε>0 в некоторой окрестности точки a имеем |f(x) – b|< ε. Т.к. |f(x) – b|=|b – f(x)| ≥|b| - |f(x)| , то |b| - |f(x)|< ε. Следовательно, |f(x)|>|b| - ε >0. Поэтому и

Z {0, ±1, ±2, ±3,...} Множество целых чисел.Множество целых чисел включает в себя множество натуральных. Q Множество рациональных чисел.Кроме целых чисел имеются ещё и дроби. Дробь - это выражение вида , где p - целое число, q - натуральное. Десятичные дроби также можно записать в виде . Например: 0,25 = 25/100 = 1/4. Целые числа также можно записать в виде . Например, в виде дроби со знаменателем "один": 2 = 2/1.Таким образом любое рациональное число можно записать десятичной дробью - конечно или бесконечной периодической. R Множество всех вещественных чисел. Иррациональные числа - это бесконечные непериодические дроби. К ним относятся: Вместе два множества (рациональных и иррациональных чисел) - образуют множество действительных (или вещественных) чисел.

Если множество не содержит ни одного элемента, то оно называется пустым множеством и записывается Ø .

Квантор существования

∃- квантор существования , используется вместо слов "существует",

"имеется". Используется также сочетание символов ∃!, которое читается как существует единственный.

Абсолютная величина

Определение. Абсолютной величиной (модулем) действительного числа называется неотрицательное число , которое определяется по формуле:

Так, например,

Свойства модуля

Если и – действительные числа, то справедливы равенства:

Функция

зависимость между двумя или большим количеством величин, при которой каждым значениям одних величин, называемых аргументами функции, ставятся в соответствие значения других величин, называемых значениями функции.

Область определения функции

Областью определения функции называют те значения независимой переменной x, при которых все операции, входящие в функцию будут выполнимы.

Непрерывная функция

Функция f (x), определенная в некоторой окрестности точки a, называется непрерывной в этой точке, если

Числовые последовательности

функция вида y = f (x ), x О N ,где N – множество натуральных чисел (или функция натурального аргумента), обозначается y = f (n )или y 1 , y 2 ,…, y n ,…. Значения y 1 , y 2 , y 3 ,…называют соответственно первым, вторым, третьим, … членами последовательности.

Предел функции непрерывного аргумента

Число А называется пределом функции y=f(x) при x->x0,если для всех значений x, достаточно мало отличающихся от числа x0, соответствующие значения функции f(x) как угодно мало отличается от числа A

Бесконечно малая функция

Функция y=f(x) называется бесконечно малой при x→a или при x →∞, если или , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.