4.1. Функциональные ряды: основные понятия, область сходимости

Определение 1 . Ряд, члены которого являются функциями одной или
нескольких независимых переменных, определёнными на некотором множестве, называется функциональным рядом .

Рассмотрим функциональный ряд , члены которого являются функциями одной независимой переменной х . Сумма первых n членов ряда является частичной суммой данного функционального ряда. Общий член есть функция от х , определённая в некоторой области. Рассмотрим функциональный ряд в точке . Если соответствующий числовой ряд сходится, т.е. существует предел частичных сумм этого ряда
(где − сумма числового ряда), то точка называется точкой сходимости функционального ряда . Если числовой ряд расходится, то точка называется точкой расходимости функционального ряда.

Определение 2 . Областью сходимости функционального ряда называется множество всех таких значений х , при которых функциональный ряд сходится. Область сходимости, состоящая из всех точек сходимости, обозначается . Отметим, что R.

Функциональный ряд сходится в области , если для любого он сходится как числовой ряд, при этом его сумма будет некоторой функцией . Это так называемая предельная функция последовательности : .

Как находить область сходимости функционального ряда ? Можно использовать признак, аналогичный признаку Даламбера. Для ряда составляем и рассматриваем предел при фиксированном х :
. Тогда является решением неравенства и решением уравнения (берём только те решения уравнения, в
которых соответствующие числовые ряды сходятся).

Пример 1 . Найти область сходимости ряда .

Решение . Обозначим , . Составим и вычислим предел , тогда область сходимости ряда определяется неравенством и уравнением . Исследуем дополнительно сходимость исходного ряда в точках, являющимися корнями уравнения:

а) если , , то получается расходящийся ряд ;

б) если , , то ряд сходится условно (по

признаку Лейбница, пример 1, лекция 3, разд. 3.1).

Таким образом, область сходимости ряда имеет вид: .

4.2. Степенные ряды: основные понятия, теорема Абеля

Рассмотрим частный случай функционального ряда, так называемый степенной ряд , где
.

Определение 3 . Степенным рядом называется функциональный ряд вида ,

где − постоянные числа, называемые коэффициентами ряда .

Степенной ряд есть «бесконечный многочлен», расположенный по возрастающим степеням . Любой числовой ряд является
частным случаем степенного ряда при .

Рассмотрим частный случай степенного ряда при :
. Выясним, какой вид имеет
область сходимости данного ряда .

Теорема 1 (теорема Абеля) . 1) Если степенной ряд сходится в точке , то он абсолютно сходится при всяком х , для которого справедливо неравенство .

2) Если же степенной ряд расходится при , то он расходится при всяком х , для которого .

Доказательство . 1) По условию степенной ряд сходится в точке ,

т. е. сходится числовой ряд

(1)

и по необходимому признаку сходимости его общий член стремится к 0, т.е. . Следовательно, существует такое число , что все члены ряда ограничены этим числом:
.

Рассмотрим теперь любое х , для которого , и составим ряд из абсолютных величин: .
Запишем этот ряд в другом виде: так как , то (2).

Из неравенства
получаем , т.е. ряд

состоит из членов, которые больше соответствующих членов ряда (2). Ряд представляет собой сходящийся ряд геометрической прогрессии со знаменателем , причём , так как . Следовательно, ряд (2) сходится при . Таким образом, степенной ряд абсолютно сходится.

2) Пусть ряд расходится при , иными словами,

расходится числовой ряд . Докажем, что для любого х () ряд расходится. Доказательство ведётся от противного. Пусть при некотором

фиксированном () ряд сходится, тогда он сходится при всех (см. первую часть данной теоремы), в частности, при , что противоречит условию 2) теоремы 1. Теорема доказана.

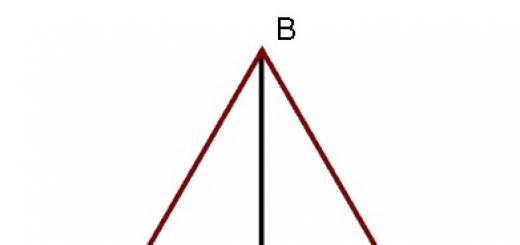
Следствие . Теорема Абеля позволяет судить о расположении точки сходимости степенного ряда. Если точка является точкой сходимости степенного ряда, то интервал заполнен точками сходимости; если точкой расходимости является точка , то
бесконечные интервалы заполнены точками расходимости (рис. 1).

Рис. 1. Интервалы сходимости и расходимости ряда

Можно показать, что существует такое число , что при всех
степенной ряд абсолютно сходится, а при − расходится. Будем считать, что если ряд сходится только в одной точке 0, то , а если ряд сходится при всех , то .

Определение 4 . Интервалом сходимости степенного ряда называется такой интервал , что при всех этот ряд сходится и притом абсолютно, а для всех х , лежащих вне этого интервала, ряд расходится. Число R называется радиусом сходимости степенного ряда.

Замечание . На концах интервала вопрос о сходимости или расходимости степенного ряда решается отдельно для каждого конкретного ряда.

Покажем один из способов определения интервала и радиуса сходимости степенного ряда.

Рассмотрим степенной ряд и обозначим .

Составим ряд из абсолютных величин его членов:

и применим к нему признак Даламбера.

Пусть существует

.

По признаку Даламбера ряд сходится, если , и расходится, если . Отсюда ряд сходится при , тогда интервал сходимости: . При ряд расходится, так как .
Используя обозначение , получим формулу для определения радиуса сходимости степенного ряда:

,

где − коэффициенты степенного ряда.

Если окажется, что предел , то полагаем .

Для определения интервала и радиуса сходимости степенного ряда также можно использовать радикальный признак Коши, радиус сходимости ряда определяется из соотношения .

Определение 5 . Обобщенным степенным рядом называется ряд вида

. Его также называют рядом по степеням .
Для такого ряда интервал сходимости имеет вид: , где − радиус сходимости.

Покажем, как находится радиус сходимости для обобщенного степенного ряда.

т.е. , где .

Если , то , и область сходимости R; если , то и область сходимости .

Пример 2 . Найти область сходимости ряда .

Решение . Обозначим . Составим предел

Решаем неравенство: , , следовательно, интервал

сходимости имеет вид: , причём R = 5. Дополнительно исследуем концы интервала сходимости:
а) , , получаем ряд , который расходится;
б) , , получаем ряд , который сходится
условно. Таким образом, область сходимости: , .

Ответ: область сходимости .

Пример 3. Ряд расходится для всех , так как при , радиус сходимости .

Пример 4. Ряд сходится при всех R, радиус сходимости .

– возможно, сложное окажется не таким уж и сложным;) Да и заголовок этой статьи тоже лукавит – ряды, о которых сегодня пойдёт речь, скорее, не сложные, а «редкоземельные». Однако от них не застрахованы даже студенты-заочники, и поэтому к данному, казалось бы, дополнительному занятию следует отнестись с максимальной серьёзностью. Ведь после его проработки вы сможете расправиться практически с любым «зверем»!

Начнём с классики жанра:

Пример 1

Во-первых, обратим внимание, что это НЕ степенной ряд (напоминаю, что оный имеет вид ) . И, во-вторых, здесь сразу бросается в глаза значение , которое заведомо не может входить в область сходимости ряда. И это уже маленький успех исследования!

Но всё-таки, как прийти к успеху большому? Спешу вас обрадовать – подобные ряды можно решать точно так же, как и степенные – опираясь на признак Даламбера или радикальный признак Коши!

Решение : значение не входит в область сходимости ряда. Это факт существенный, и его нужно обязательно отметить!

Основой же алгоритм работает стандартно. Используя признак Даламбера, найдём интервал сходимости ряда:

Ряд сходится при . Поднимем модуль наверх:

Сразу проконтролируем «нехорошую» точку: значение не вошло в область сходимости ряда.

Исследуем сходимость ряда на «внутренних» концах интервалов:
если , то
если , то

Оба числовых ряда расходятся, так как не выполнен необходимый признак сходимости .

Ответ : область сходимости:

Выполним небольшую аналитическую проверку. Давайте подставим в функциональный ряд какое-нибудь значение из правого интервала, например, :
– сходится по признаку Даламбера .

В случае подстановки значений из левого интервала тоже получаются сходящиеся ряды:
если , то .

И, наконец, если , то ряд – действительно расходится.

Пара простеньких примера для разогрева:

Пример 2

Найти область сходимости функционального ряда

Пример 3

Найти область сходимости функционального ряда

Особенно хорошо разберитесь с «новым» модулем – он сегодня встретится 100500 раз!

Краткие решения и ответы в конце урока.

Использованные алгоритмы вроде бы универсальны и безотказны, но на самом деле это не так – для многих функциональных рядов они часто «пробуксовывают», а то и приводят к ошибочным выводам (и такие примеры я тоже рассмотрю) .

Шероховатости начинаются уже на уровне интерпретации результатов: рассмотрим, например, ряд . Здесь в пределе получаем (проверьте самостоятельно) , и по идее нужно дать ответ, что ряд сходится в единственной точке. Однако, точка «заиграна», а значит, наш «пациент» расходится вообще всюду!

А для ряда «очевидное» решение «по Коши» вообще ничего не даёт:
– для ЛЮБОГО значения «икс».

И возникает вопрос, что же делать? Используем метод, которому как раз будет посвящена основная часть урока! Его можно сформулировать следующим образом:

Прямой анализ числовых рядов при различных значениях

Фактически мы уже начали этим заниматься в Примере 1. Сначала исследуем какое-нибудь конкретное «икс» и соответствующий числовой ряд. Напрашивается взять значение :
– полученный числовой ряд расходится.

И это сразу наталкивает на мысль: а что, если то же самое происходит и в других точках?
Проверим-ка необходимый признак сходимости ряда для произвольного значения :

Точка учтена выше, для всех же остальных «икс» стандартным приёмом организуем второй замечательный предел :

Вывод : ряд расходится на всей числовой прямой

И это решение – самый что ни на есть рабочий вариант!

На практике функциональный ряд часто приходится сопоставлять с обобщённым гармоническим рядом :

Пример 4

Решение : прежде всего, разбираемся с областью определения : в данном случае подкоренное выражение должно быть строго положительным, и, кроме того, должны существовать все члены ряда, начиная с 1-го. Из этого следует то, что:
. При этих значениях получаются условно сходящиеся ряды :
и т.д.

Другие же «икс» не годятся, так, например, при мы получим нелегальный случай , где не существует первых двух членов ряда.

Это всё хорошо, это всё понятно, но остаётся ещё один немаловажный вопрос – как грамотно оформить решение? Я предлагаю схему, которую можно жаргонно назвать «перевод стрелок» на числовые ряды :

Рассмотрим произвольное значение и исследуем сходимость числового ряда . Рутинный признак Лейбница :

1) Данный ряд является знакочередующимся.

2) – члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше, чем предыдущий: , значит, убывание монотонно.

Вывод: ряд сходится по признаку Лейбница. Как уже отмечалось, сходимость тут условная – по той причине, что ряд – расходится.

Вот так вот – аккуратно и корректно! Ибо за «альфой» мы хитро спрятали все допустимые числовые ряды.

Ответ : функциональный ряд существует и сходится условно при .

Аналогичный пример для самостоятельного решения:

Пример 5

Исследовать сходимость функционального ряда

Примерный образец чистового оформления задания в конце урока.

Вот тебе и «рабочая гипотеза»! – на интервале функциональный ряд сходится!

2) С симметричным интервалом всё прозрачно, рассматриваем произвольные значения и получаем: – абсолютно сходящиеся числовые ряды.

3) И, наконец, «серединка» . Здесь тоже удобно выделить два промежутка.

Рассматриваем произвольное значение из интервала и получаем числовой ряд:

! Опять же – если трудно , подставляйте какое-нибудь конкретное число, например . Впрочем,… вы же хотели трудностей =)

Для всех значений «эн» выполнено , значит:
– таким образом, по признаку сравнения ряд сходится вместе с бесконечно убывающей прогрессией .

Для всех значений «икс» из интервала получаем – абсолютно сходящиеся числовые ряды.

Все «иксы» исследованы, «иксов» больше нет!

Ответ : область сходимости ряда:

Надо сказать, неожиданный результат! И ещё следует добавить, что использование признаков Даламбера или Коши здесь однозначно введёт в заблуждение!

Прямая оценка – это «высший пилотаж» математического анализа, но для этого, конечно, требуется опыт, а где-то даже и интуиция.

А может быть кто-то найдёт путь проще? Пишите! Прецеденты, кстати, есть – несколько раз читатели предлагали более рациональные решения, и я с удовольствием их публиковал.

Успешного вам приземления:)

Пример 11

Найти область сходимости функционального ряда

Моя версия решения совсем близко.

Дополнительный хардкор можно найти в Разделе VI (Ряды) сборника Кузнецова (Задачи 11-13). В Интернете есть готовые решения , но здесь я должен вас предостеречь – многие из них неполные, некорректные, а то и вообще ошибочные. И, к слову, это была одна из причин, по которой появилась на свет данная статья.

Давайте подведём итоги трёх уроков и систематизируем наш инструментарий. Итак:

Чтобы найти интервал(ы) сходимости функционального ряда, можно использовать :

1) Признак Даламбера или признак Коши . И если ряд не степенной – проявляем повышенную осторожность, анализируя полученный результат прямой подстановкой различных значений .

2) Признак равномерной сходимости Вейерштрасса . Не забываем!

3) Сопоставление с типовыми числовыми рядами – рулит в общем случае.

После чего исследуем концы найденных интервалов (если нужно) и получаем область сходимости ряда.

Теперь в вашем распоряжении довольно-таки серьёзный арсенал, который позволит справиться практически с любым тематическим заданием.

Желаю успехов!

Решения и ответы:

Пример 2: Решение : значение не входит в область сходимости ряда.
Используем признак Даламбера:


Ряд сходится при:

Таким образом, интервалы сходимости функционального ряда: .
Исследуем сходимость ряда в конечных точках:
если , то ;
если , то .
Оба числовых ряда расходятся, т.к. не выполнен необходимый признак сходимости.

Ответ : область сходимости:

Функциональным рядом называется формально записанное выражение

u 1 (x ) + u 2 (x ) + u 3 (x ) + ... + u n (x ) + ... , (1)

где u 1 (x ), u 2 (x ), u 3 (x ), ..., u n (x ), ... - последовательность функций от независимой переменной x .

Сокращённая запись функционального ряда с сигмой: .

Примерами функциональных рядов могут служить :

(2)

(3)

Придавая независимой переменной x некоторое значение x 0 и подставляя его в функциональный ряд (1), получим числовой ряд

u 1 (x 0 ) + u 2 (x 0 ) + u 3 (x 0 ) + ... + u n (x 0 ) + ...

Если полученный числовой ряд сходится, то говорят, что функциональный ряд (1) сходится при x = x 0 ; если он расходится, что говорят, что ряд (1) расходится при x = x 0 .

Пример 1. Исследовать сходимость функционального ряда (2) при значениях x = 1 и x = - 1 .
Решение. При x = 1 получим числовой ряд

который сходится по признаку Лейбница. При x = - 1 получим числовой ряд

,

который расходится как произведение расходящегося гармонического ряда на – 1. Итак, ряд (2) сходится при x = 1 и расходится при x = - 1 .

Если такую проверку на сходимость функционального ряда (1) осуществить относительно всех значений независимой переменной из области определения его членов, то точки этой области разобьются на два множества: при значениях x , взятых в одном из них, ряд (1) сходится, а в другом – расходится.

Множество значений независимой переменной, при которых функциональный ряд сходится, называется его областью сходимости .

Пример 2. Найти область сходимости функционального ряда

Решение. Члены ряда определены на всей числовой прямой и образуют геометрическую прогрессию со знаменателем q = sin x . Поэтому ряд сходится, если

и расходится, если

(значения невозможны). Но при значениях и при остальных значениях x . Следовательно, ряд сходится при всех значениях x , кроме . Областью его сходимости служит вся числовая прямая, за исключением этих точек.

Пример 3. Найти область сходимости функционального ряда

Решение. Члены ряда образуют геометрическую прогрессию со знаменателем q =lnx . Поэтому ряд сходится, если , или , откуда . Это и есть область сходимости данного ряда.

Пример 4. Исследовать сходимость функционального ряда

Решение. Возьмём произвольное значение . При этом значении получим числовой ряд

(*)

Найдём предел его общего члена

Следовательно, ряд (*) расходится при произвольно выбранном, т.е. при любом значении x . Область его сходимости – пустое множество.

Равномерная сходимость функционального ряда и её свойства

Перейдём к понятию равномерной сходимости функционального ряда . Пусть s (x ) - сумма этого ряда, а s n (x ) - сумма n первых членов этого ряда. Функциональный ряд u 1 (x ) + u 2 (x ) + u 3 (x ) + ... + u n (x ) + ... называется равномерно сходящимся на отрезке [a , b ] , если для любого как угодно малого числа ε > 0 найдётся такой номер N , что при всех n ≥ N будет выполнятся неравенство

|s (x ) − s n (x )| < ε

для любого x из отрезка [a , b ] .

Приведённое выше свойство можно геометрически иллюстрировать следующим образом.

Рассмотрим график функции y = s (x ) . Построим около этой кривой полосу шириной 2ε n , то есть построим кривые y = s (x ) + ε n и y = s (x ) − ε n (на рисунке ниже они зелёного цвета).

Тогда при любом ε n график функции s n (x ) будет лежать целиком в рассматриваемой полосе. В этой же полосе будут лежать графики всех последующих частичных сумм.

Всякий сходящийся функциональный ряд, который не обладает описанным выше признаком - неравномерно сходящийся.

Рассмотрим ещё одно свойство равномерно сходящихся функциональых рядов:

сумма ряда непрерывных функций, равномерно сходящегося на некотором отрезке [a , b ] , есть функция, непрерывная на этом отрезке .

Пример 5. Определить, непрерывна ли сумма функционального ряда

Решение. Найдём сумму n первых членов этого ряда:

Если x > 0 , то

,

если x < 0 , то

если x = 0 , то

И поэтому .

Наше исследование показало, что сумма данного ряда - разрывная функция. Её график изображён на рисунке ниже.

Признак Вейерштрасса равномерной сходимости функциональных рядов

К признаку Вейерштрасса подойдём через понятие мажоририуемости функциональных рядов . Функциональный ряд

u 1 (x ) + u 2 (x ) + u 3 (x ) + ... + u n (x ) + ...

Пусть функция определена в области

Определение. Выражение

Называется функциональным рядом.

Пример.

При одних значениях ряд может сходиться, для других значений – расходиться.

Пример.

Найдите область сходимости ряда . Данный ряд определен для значений

Если то , ряд расходится, так как не выполняется необходимый признак сходимости ряда; если ряд расходится; если - бесконечно убывающая геометрическая прогрессия.

Сравнение данного ряда со сходящимся рядом при дает область сходимости исследуемого ряда .

При значениях из функционального ряда получается числовой ряд

Если для числовой ряд сходится, то точка называется точкой сходимости функционального ряда.

Совокупность всех точек сходимости ряда образует область его сходимости. Областью сходимости обычно бывает какой-нибудь интервал оси .

Если в каждой точке числовые ряды сходятся, то функциональный ряд называется сходящимся в области .

Сумма функционального ряда является некоторой функцией от переменной , определенной в области сходимости ряда

Какими свойствами обладают функции , если известны свойства членом ряда, то есть .

Непрерывность функций не достаточна для того, чтобы сделать заключение о непрерывности .

Сходимость ряда непрерывных функций к непрерывной же функции обеспечивается дополнительным условием, выражающим одну важную особенность сходимости функционального ряда.

Определение . Функциональный ряд называется сходящимся в области , если существует предел частичных сумм этого ряда, то есть .

Определение . Функциональный ряд называется равномерно сходящимся в области , если для любого положительного , найдется такое число , что для всех выполняется неравенство .

Геометрический смысл равномерной сходимости

Если окружить график функции - полоской”, определяемой соотношением то графики всех функций , начиная с достаточно большого значения , целиком лежат в этой « - полоске», окружающей график предельной функции .

Свойства равномерно сходящегося ряда .

1. Сумма равномерно сходящегося ряда в некоторой области , составленного из непрерывных функций, является функцией непрерывной в этой области.

2. Такой ряд можно почленно дифференцировать

3. Ряд можно почленно интегрировать

Для того чтобы определить является ли функциональный ряд равномерно сходящимся, надо воспользоваться достаточным признаком сходимости Вейерштрасса.

Определение . Функциональный ряд называется мажорируемым в некоторой области изменения , если существует такой сходящийся числовой ряд с положительными членами, что для всех из этой области выполняются неравенства .

Признак Вейерштрасса (равномерной сходимости функционального ряда).

Функциональный ряд сходится равномерно в области сходимости, если он является мажорируемым в этой области.

Другими словами, если функции в некоторой области не превосходят по абсолютной величине соответствующих положительных чисел и если числовой ряд сходится, то функциональный ряд в этой области сходится равномерно.

Пример . Доказать равномерную сходимость функционального ряда .

Решение . . Заменим общий член этого ряда общим членом числового ряда, но превосходящего каждый член ряда по абсолютной величине. Для этого надо определить , при котором общий член ряда будет максимальным.

Полученный числовой ряд сходится, значит, функциональный ряд сходится равномерно согласно признаку Вейерштрасса.

Пример . Найдите сумму ряда .

Для нахождения суммы ряда воспользуемся известной формулой для суммы геометрической прогрессии

Дифференцируя левую и правую части формулы (1), получим последовательно

Выделим в сумме, подлежащей вычислению, слагаемые, пропорциональные первой и второй производной:

Вычислим производные:

Степенные ряды.

Среди функциональных рядов есть класс степенных и тригонометрических рядов.

Определение . Функциональный ряд вида

называется степенным по степеням . Выражения - постоянные числа.

Если ряд является степенным по степеням .

Область сходимости степенного ряда. Теорема Абеля.

Теорема . Если степенной ряд сходится в точке , то он сходится и притом абсолютно для всякого значения , по абсолютной величине меньшего , то есть или в интервале .

Доказательство.

Вследствие сходимости рада его общий член должен стремиться к нулю, поэтому все члены этого ряда равномерно ограничены: существует такое постоянное положительное число , что при всяком имеет место неравенство ., что для всех с центром в точке