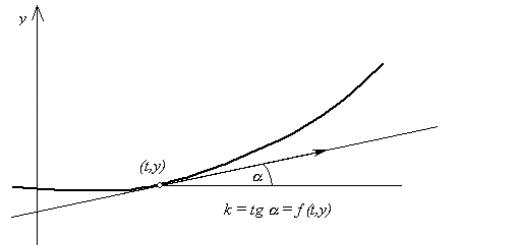
Если в электростатическом поле точечного заряда Q из точки1 в точку2 вдоль произвольной траектории (рис. 132) перемещается другой точечный зарядQ 0 , то сила, приложенная к заряду, совершает работу. Работа силы F на элементарном перемеще­нии dl равна

Так как d/cos=dr , то

Работа при перемещении заряда Q 0 из точки1 в точку2

(83.1)

не зависит от траектории перемещения, а определяется только положениями начальной 1 и конечной2 точек. Следовательно, электростатическое поле точечного заряда являетсяпотенциальным , а электростатические силы -консервативными (см. § 12).

Из формулы (83.1) следует, что работа, совершаемая при перемещении электричес­кого заряда во внешнем электростатическом поле по любому замкнутому пути L , равна нулю, т.е.

Если в качестве заряда, переносимого в электростатическом поле, взять единичный точечный положительный заряд, то элементарная работа сил поля на пути dl равнаЕ dl =E l dl , гдеE l =E cos - проекция вектораЕ на направление элементарного переме­щения. Тогда формулу (83.2) можно записать в виде

(83.3)

Интеграл называется циркуляцией вектора напряженности. Следователь­но, циркуляция вектора напряженности электростатического поля вдоль любого за­мкнутого контура равна нулю. Силовое поле, обладающее свойством (83.3), называет­ся потенциальным. Из обращения в нуль циркуляции вектораЕ следует, что линии напряженности электростатического поля не могут быть замкнутыми, они начинаются и кончаются на зарядах (соответственно на положительных или отрицательных) или же уходят в бесконечность.

Формула (83.3) справедлива только для электростатического поля. В дальнейшем будет показано, что для поля движущихся зарядов условие (83.3) не выполняется (для него циркуляция вектора напряженности отлична от нуля).

§ 84. Потенциал электростатического поля

Тело, находящееся в потенциальном поле сил (а электростатическое поле является потенциальным), обладает потенциальной энергией, за счет которой силами поля совершается работа (см. § 12). Как известно (см. (12.2)), работа консервативных сил совершается за счет убыли потенциальной энергии. Поэтому работу (83.1) сил электро­статического поля можно представить как разность потенциальных энергий, которыми обладает точечный заряд Q 0 в начальной и конечной точках поля зарядаQ :

(84.1)

откуда следует, что потенциальная энергия заряда qq в поле зарядаQ равна

Она, как и в механике, определяется неоднозначно, а с точностью до произвольной постоянной С . Если считать, что при удалении заряда в бесконечность (r ) потенци­альная энергия обращается в нуль (U =0), тоС =0 и потенциальная энергия зарядаQ 0 , находящегося в поле зарядаQ на расстоянии г от него, равна

(84.2)

Для одноименных зарядов Q 0 Q > 0 и потенциальная энергия их взаимодействия (оттал­кивания) положительна, для разноименных зарядовQ 0 Q <0 и потенциальная энергия их взаимодействия (притяжения) отрицательна.

Если поле создается системой n точечных зарядовQ 1 , Q 2 , ..., Q n , то работа электростатических сил, совершаемая над зарядомQ 0 , равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности. Поэтому потенциальная энергияU зарядаQ 0 , находящегося в этом поле, равна сумме потенциальных энергийU i , каждого из зарядов:

(84.3)

Из формул (84.2) и (84.3) вытекает, что отношение U / Q 0 не зависит отQ 0 и является поэтомуэнергетической характеристикой электростатического поля, называемой по­тенциалом:

Потенциал  в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещен­ного в эту точку.

Из формул (84.4) и (84.2) следует, что потенциал поля, создаваемого точечным зарядом Q , равен

Работа, совершаемая селами электростатического поля при перемещении заряда Q 0 из точки1 в точку2 (см. (84.1), (84.4), (84.5)), может быть представлена как

т. е. равна произведению перемещаемого заряда на разность потенциалов в начальной и конечной точках. Разность потенциалов двух точек1 и2 в электростатическом поле определяется работой, совершаемой силами поля, при перемещении единичного поло­жительного заряда из точки1 в точку2 .

Работа сил поля при перемещении заряда Q 0 из точки1 в точку2 может быть записана также в виде

(84.7)

Приравняв (84.6) и (84.7), придем к выражению для разности потенциалов:

(84.8)

где интегрирование можно производить вдоль любой линии, соединяющей начальную и конечную точки, так как работа сил электростатического поля не зависит от траек­тории перемещения.

Если перемещать заряд Q 0 из произвольной точки за пределы поля, т. е. в бесконеч­ность, где, по условию, потенциал равен нулю, то работа сил электростатического поля, согласно (84.6),A  = Q 0  , откуда

Таким образом, потенциал - физическая величина, определяемая работой по переме­щению единичного положительного заряда при удалении его из данной точки поля в бесконечность. Эта работа численно равна работе, совершаемой внешними силами (против сил электростатического поля) по перемещению единичного положительного заряда из бесконечности в данную точку поля.

Из выражения (84.4) следует, что единица потенциала - вольт (В): 1 В есть потен­циал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией 1 Дж (1 В= 1 Дж/Кл). Учитывая размерность вольта, можно показать, что введенная в § 79 единица напряженности электростатического поля действительно равна 1 В/м: 1 Н/Кл=1 Нм/(Клм)=1 Дж/(Клм)=1 В/м.

Из формул (84.3) и (84.4) вытекает, что если поле создается несколькими зарядами, то потенциал поля системы зарядов равен алгебраической сумме потенциалов полей всех этих зарядов:

При перемещении заряда по произвольному замкнутому пути L работа сил электростатического поля равна нулю. Поскольку, конечное положение заряда равно начальному r 1 =r 2 , то и (кружок у знака интеграла указывает на то, что интегрирование производится по замкнутому пути). Так как и , то . Отсюда получаем . Сократив обе части равенства на q 0 , получим или , где E l =Ecosa - проекция вектора Е на направление элементарного перемещения . Интеграл называется циркуляцией вектора напряженности . Таким обра­зом, циркуляция вектора напряженности электростатического поля вдоль лю­бого замкнутого контура равна нулю . Это заключение есть условие потенциаль­ности поля .

Потенциальная энергия заряда.

В потенциальном поле тела обладают потенциальной энергией и работа консервативных сил совершается за счет убыли потенциальной энергии.

Поэтому работу A 12 можно представить, как разность потенциальных энергий заряда q 0 в начальной и конечной точках поля заряда q :

Потенциальная энергия заряда q 0 , находящегося в поле заряда q на расстоянии r от него равна

Считая, что при удалении заряда на бесконечность, потенциальная энергия обращается в нуль, получаем: const = 0 .

Для одноименных зарядов потенциальная энергия их взаимодействия (отталкивания) положительна , для разноименных зарядов потенциальная энергия из взаимодействия (притяжения ) отрицательна .

Если поле создается системой n точечных зарядов, то потенциальная энергия заряда q 0 , находящегося в этом поле, равна сумме его потенциальных энергий, создаваемых каждым из зарядов в отдельности:

Потенциал электростатического поля.

Отношение не зависит от пробного заряда q0 и является, энергетической характеристикой поля, называемой потенциалом :

Потенциал ϕ в какой-либо точке электростатического поля есть скалярная физическая величина , определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку.

1.7 Связь между напряженностью и потенциалом.

Связь между потенциалом и напряженностью электростатического поля. Эквипотенциальные поверхности.

Как ранее показано, работа сил электростатического поля при перемещении за­ряда q 0 может быть записана с одной стороны, как , с другой же - как убыль потенциальной энергии, т.е. . Здесь dr - есть проекция элементарного перемещения dl заряда на направление силовой линии , - есть малая разность потенциалов двух близко расположенных точек поля. Приравняем правые части равенств и сократим на q 0 . Получаем соотношения , . Отсюда .

Последнее соотношение представляет связь ос­новных характеристик электро­статического поля Е и j. Здесь - быстрота изменения потенциала в направле­нии силовой линии. Знак ми­нус указывает на то, что вектор направлен в сторону убывания потенциала. Поскольку , можно записать проекции вектора на координатные оси: . Отсюда следует, что . Выраже­ние, стоящее в скобках, называется градиентом скаляра j и обозначается как gradj.

Напряженность электростатического поля равна гра­диенту потенциала, взя­тому с обратным знаком .

Для графического изображения распределения потенциала электростатичес­кого поля пользуются эквипотенциальными поверхностями - поверхностями, потен­циал всех точек которых одинаков . Потенциал поля одиночного точечного заряда . Эквипотенциальные поверх­нос­ти в данном случае есть концентрические сферы с центром в точке расположе­ния за­ряда q (рис.1.13). Эквипотенциальных поверхностей можно провести бесконеч­ное множество, однако принято чертить их с густотой, пропорциональной величине Е.

1.8 Электроемкость, плоский конденсатор.

Электроемкость.

Рассмотрим уединенный проводник - проводник, удаленный от других тел и зарядов. Из опыта следует, что разные проводники, будучи одинаково заряженными, имеют разные потенциалы.

Физическая величина C , равная отношению заряда проводника q к его потенциалу ϕ , называется электрической емкостью этого проводника.

Электроемкость уединенного проводника численно равна заряду, который нужно сообщить этому проводнику для того, чтобы изменить его потенциал на единицу.

Она зависит от формы и размеров проводника и от диэлектрических свойств окружающей среды. Емкости геометрически подобных проводников пропорциональны их линейным размерам.

Пример : Рассмотрим уединенный шар радиуса R, находящийся в однородной среде с диэлектрической проницаемостью e. Ранее было получено, что потенциал шара ра­вен . Тогда емкость шара , т.е. зависит только от его ра­диуса.

Единица электроемкости -фарад(Ф):1Ф-емкость такогоуединенного проводника, потенциал которого изменяется на 1В при сообщении ему заряда 1Кл. Емкостью 1Ф обладает шар с радиусом R = 9 ⋅10 6 км. Емкость Земли 0,7мФ.

Рассмотрим некоторые следствия из установленного принципа.

Если - произвольное электростатическое поле, - направленный отрезок контура , то работу электростатического поля по бесконечно медленному перемещению положительного единичного точечного заряда можно описать с помощью криволинейного интеграла

. (1)

Циркуляцией вектора по замкнутому контуру называют скалярную величину

Здесь угол - угол между направлением вектора и направленным элементарным отрезком контура , - проекция вектора на направление , величина является модулем элементарного направленного отрезка контура . В определение циркуляции обязательно входит указание направления обхода контура. Очевидно, что изменение направления обхода приводит к смене алгебраического знака циркуляции. Заметим, что формальное определение понятия «циркуляция векторного поля» (2) не связано с физическим перемещением заряда по траектории: в нестационарном случае величина циркуляции рассчитывается для фиксированного момента времени, одного и того же для всех точек контура. При описании реального движения заряда пришлось бы учитывать, что вместе с изменением положения заряда изменялось бы и время наблюдения. В этой связи полезно помнить высказывание нобелевского лауреата по физике Р. Фейнмана о том, что абстрактное математическое представление зачастую оказывается и самым полным и самым правильным и самым содержательным.

Специального общепринятого символьного обозначения для циркуляции векторного поля не существует, а содержание понятия становится ясным из рассмотрения выражения

, (3)

где - длина контура . Теперь можно сформулировать интуитивное определение циркуляции векторного поля по замкнутому контуру конечной длины:

В силу установленного выше принципа потенциальности электростатического поля выражение (2) должно обращаться в нуль для любого замкнутого контура :

Условие (4) играет важную роль в электростатике: в реально существующем электростатическом поле обязательно выполнено интегральное условие потенциальности (4).

Обратим внимание читателя на то, что из условия (4) следует важный физический результат: силовые линии напряжённости электростатического поля не могут быть замкнутыми и не могут пересекаться, в противном случае условие (4) было бы несправедливо. Силовые линии или «замыкаются» на электрический заряд, или уходят «на бесконечность». В связи со сказанным следует отметить, что выбранное положительное направление вдоль силовой линии не может измениться на противоположное ни в одной точке пространства, через которую проходит рассматриваемая силовая линия.

Рассмотрим перемещение единичного положительного сосредоточенного электрического заряда из произвольной точки пространства А в произвольную точку В по двум произвольным траекториям и (рис.1). Справедливо утверждение, что

Поле Е обладает двумя чрезвычайно важными свойствами, знание которых помогло глубже проникнуть в суть самого понятия поля и сформировать его законы. Эти свойства - теорема Гаусса и теорема о циркуляции вектора Е - связаны с двумя важнейшими математическими характеристиками всех векторных полей: циркуляцией и потоком . Пользуясь только этими двумя понятиями можно описать все законы. Рассмотрим эти свойства.

Из механики известно, что любое стационарное поле центральных сил является консервативным, т.е. работа сил этого поля не зависит от пути, а определяется только положением начальной и конечной точек перемещения. Именно таким свойством обладает электростатическое поле - поле, образованное системой неподвижных точечных зарядов.

1. Рассчитаем работу при перемещении точечного заряда в электростатическом поле.

Пусть электростатическое поле создано зарядом + Q. Будем перемещать другой точечный заряд q (q – пробный положительный точечный заряд) в электростатическом поле, созданном зарядом (+Q) из точки 1 в точку 2 по произвольной траектории (смотри рис. 6.1.). Работу будет совершать сила F К – кулоновская сила, действующая на заряд q . Работа силыF К на элементарном перемещении dl равна:

Рис.6.1.Работа перемещения точечного заряда в электростатическом поле

Для нахождения работы перемещения заряда q из точки 1 в точку 2 проинтегрируем (6.2) по переменной r .

Работа перенесения заряда q из точки 1 в точку 2 не зависит от траектории перемещения, а определяется только положениями начальной и конечной точек перемещения, следовательно , электростатическое поле точечного заряда является потенциальным, а кулоновские силы – консервативными.

Покажем, что работа сил ЭС поля по любому замкнутому пути равна 0 .

Пусть перемещается положительный единичный заряд q из точки 1 в неё же по замкнутому пути - 1а2b1- замкнутый контур Г (рис.6.2) . Согласно соотношению (6.3) работа будет равна 0, т.к. r 1 = r 2 . Но, с другой стороны величину этой работы можем записать, используя связь между кулоновской силой и вектором напряженности электростатического поля (q ) в виде:

Но, модуль вектора напряженности точечного заряда равен kQ/r 2 =| |, следовательно элементарную работу сил электростатического поля можно представить в виде выражения:

Интеграл r dr = - называют циркуляцией вектора Е .

Теорема о циркуляции вектора Е: Циркуляция вектора напряженности электростатического поля по произвольному замкнутому контуру тождественно равна нулю.

Теорема о циркуляции

Ранее мы выяснили, что на заряд (q), который находится в электростатическом поле, действуют консервативные силы, работа ($A$) которых на любом замкнутом пути (L) равна нулю:

где $\overrightarrow{s}$- вектор перемещения (не путать с площадью), $\overrightarrow{E}$ -- вектор напряженности поля.

Для единичного положительного заряда можем записать:

Интеграл в левой части уравнения (2) есть циркуляция вектора напряженности по контуру L. Характерным свойством электростатического поля является то, что циркуляция его вектора напряжённости по любому замкнутому контуру равна нулю. Такое утверждение называется теоремой о циркуляции вектора напряженности электростатического поля.

Докажем теорему о циркуляции на том основании, что работа поля по перемещению заряда не зависит от траектории перемещения заряда в электростатическом поле, что выражается равенством:

где $L_1\ и\ L_2$ различные пути между точками А и В. Учтем, что при замене местами пределов интегрирования получим:

Выражение (4) представим как:

где $L=L_1+L_2$. Так теорема доказана.

Следствием теоремы о циркуляции является то, что линии напряженности электростатического поля незамкнуты. Они начинаются на положительных зарядах, а заканчиваются на отрицательных или уходят в бесконечность. Теорема верна именно для статичных зарядов. Другое следствие теоремы: непрерывность тангенциальных составляющих напряженности (в отличие от нормальных составляющих). Это значит, что компоненты напряженности, которые являются касательными к выбранной любой поверхности во всякой ее точке, имеют по обе стороны поверхности равные значения.

Выделим произвольную поверхность S, которая опирается на контур L (рис.1).

В соответствии с формулой Стокса (теоремой Стокса) интеграл от ротора вектора напряженности ($rot\overrightarrow{E}$), взятый по поверхности S равен циркуляции вектора напряженности вдоль контура, на который опирается данная поверхность:

где $d\overrightarrow{S}=dS\cdot \overrightarrow{n}$, $\overrightarrow{n}$ -- единичный вектор перпендикулярный участку dS. Ротор ($rot\overrightarrow{E}$) характеризует интенсивность «завихрения» вектора. Наглядное представление о роторе вектора можно получить, если маленькую легкую крыльчатку (рис.2) поместить в поток жидкости. В тех местах, где ротор не равен нулю, крыльчатка будет вращаться, причем скорость ее вращения будет тем больше, чем больше проекция модуль проекции ротора на ось крыльчатки.

При практическом вычислении ротора чаще других используют формулы:

Так как в соответствии с уравнением (6) циркуляция вектора напряжённости равна нулю, то мы получаем:

Условие (8) должно выполняться для любой поверхности S, которая опирается на контур L. Это возможно только в том случае, если подынтегральное выражение:

причем для каждой точки поля.

По аналогии с крыльчаткой на рис. 2 представим себе электрическую «крыльчатку». На концах такой «крыльчатки» расположены одинаковые по величине заряды q. Система помещена в однородное поле с напряженностью E. В тех местах, где $rot\overrightarrow{E}\ne 0$ такое «устройство» будет вращаться с ускорением, которое зависит от проекции ротора на ось крыльчатки. В случае, электростатического поля такое «устройство» не стало бы вращаться ни при какой ориентации оси. Так как отличительной особенностью электростатического поля является то, что оно безвихревое. Уравнение (9) представляет теорему о циркуляции в дифференциальной форме.

Пример 1

Задание: На рис. 3 изображено электростатическое поле. Что можно сказать о характеристиках данного поля из рисунка?

О данном поле можно сказать, что существование такого электростатического поля невозможно. Если выделить контур (он изображен пунктиром). Для такого контура циркуляция вектора напряженности:

\[\oint\limits_L{\overrightarrow{E}d\overrightarrow{s}\ne 0}\left(1.1\right),\]

что противоречит теореме о циркуляции для электростатического поля. Напряженность поля определяется густотой силовых линий, она в разных частях поля не одинакова, в результате работа по замкнутому контуру будет отличаться от нуля, следовательно, циркуляция вектора напряженности не равна нулю.

Пример 2

Задание: Исходя из теоремы о циркуляции, покажите, что тангенциальные составляющие вектора напряженности электростатического поля не изменяются при переходе через границу раздела диэлектриков.

Рассмотрим границу между двумя диэлектриками с диэлектрическими проницаемостями ${\varepsilon }_2\ и\ {\varepsilon }_1$ (рис.4). Выберем на этой границе небольшой прямоугольный контур с параметрами a - длина, b - ширина. Ось Х проходит через середины сторон b.

Для электростатического поля выполняется теорема о циркуляции, которая выражается уравнением:

\[\oint\limits_L{\overrightarrow{E}d\overrightarrow{s}=0\ \left(2.1\right).}\]

При небольших размерах контура циркуляция вектора напряженности и в соответствии с указанным направлением обхода контура интеграл в формуле (2.1) можно представить как:

\[\oint\limits_L{\overrightarrow{E}d\overrightarrow{s}=E_{1x}a-E_{2x}a+\left\langle E_b\right\rangle 2b=0\ \left(2.2\right),}\]

где $\left\langle E_b\right\rangle $- среднее значение $\overrightarrow{E}$ на участках перпендикулярных к границе раздела.

Из (2.2) следует, что:

\[{(E}_{2x}-E_{1x})a=\left\langle E_b\right\rangle 2b\ (2.3).\]

Если $b\to 0$, то получаем, что:

Выражение (2.4) выполняется при произвольном выборе оси X, которая лежит на границе раздела диэлектриков. Если представить вектор напряженности в виде двух составляющих (тангенциальной $E_{\tau }\ $ и нормальной $E_n$):

\[\overrightarrow{E_1}=\overrightarrow{E_{1n}}+\overrightarrow{E_{1\tau }},\overrightarrow{E_2}=\overrightarrow{E_{2n}}+\overrightarrow{E_{2\tau }}\ \left(2.5\right).\]

В таком случае из (2.4) запишем:

где $E_{\tau i}$- проекция вектора напряженности на орт $\tau $, направленный вдоль границы раздела диэлектриков.