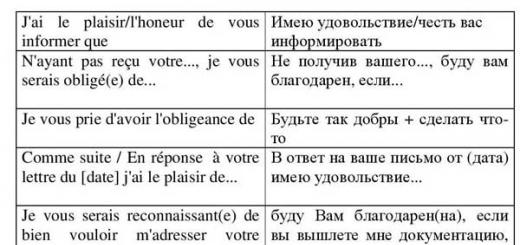
Для опытов со струной удобен прибор, изображенный на рис. 98. Один коней струны закреплен, а другой перекинут через блок, и к нему можно подвешивать тот или иной груз. Таким образом, сила натяжения струны нам известна: она равна весу груза. Доска, над которой натянута струна, снабжена шкалой. Это позволяет быстро определить длину всей струны или какой-либо ее части.
Рис. 98. Прибор для исследования колебаний струны
Оттянув струну посередине и отпустив, мы возбудим в ней колебание, изображенное на рис. 99, а. На концах струны получаются узлы, посередине - пучность.
Рис. 99. Свободные колебания струны: а) с одной пучностью; б) с двумя пучностями; в) с тремя пучностями
С помощью этого прибора, меняя массу груза, натягивающего струну, и длину струны (перемещая добавочный зажим со стороны закрепленного конца), нетрудно экспериментально установить, чем определяется собственная частота колебания струны. Эти опыты показывают, что частота колебания струны прямо пропорциональна корню квадратному из силы натяжения струны и обратно пропорциональна длине струны, т. е.
Что касается коэффициента пропорциональности, то он зависит, как оказывается, только от плотности того материала, из которого сделана струна, и от толщины струны , а именно он равен . Таким образом, собственная частота колебаний струны выражается формулой
В струнных инструментах сила натяжения создается, конечно, но подвешиванием грузов, а растягиванием струны при накручивании одного из ее концов ни вращающийся стерженек (колок). Поворотом колка, т. е. изменением силы натяжения , осуществляется и настройка струны на требуемую частоту.
Поступим теперь следующим образом. Оттянем одну половинку струны вверх, а другую - вниз с таким расчетом, чтобы средняя точка струны не сместилась. Отпустив одновременно обе оттянутые точки струны (отстоящие от концов струны на четверть ее длины), мы увидим, что в струне возбудится колебание, имеющее, кроме двух узлов на концах, еще узел посередине (рис. 99, б) и, следовательно, две пучности. При таком свободном колебании звук струны получается в два раза выше (на октаву выше, как принято говорить в акустике), чем при предыдущем колебании с одной пучностью, т. е. частота равна теперь . Струна как бы разделилась на две более короткие струны, натяжение которых прежнее.
Можно возбудить далее колебание с двумя узлами, делящими струну на три равные части, т. е. колебание с тремя пучностями (рис. 99, в). Для этого нужно оттянуть струну в трех точках, как показано стрелками на рис. 99, в. Частота этого колебания равна . Оттягивая струну в нескольких точках, трудно получить колебания с еще большим числом узлов и пучностей, но такие колебания возможны. Их удается возбудить, например, проводя по струне смычком в том месте, где должна получиться пучность, и слегка придерживая пальцами ближайшие узловые точки. Такие свободные колебания с четырьмя, пятью пучностями и т. д. имеют частоты и т. д.
Итак, у струны имеется целый набор колебаний и соответственно целый набор собственных частот, кратных наиболее низкой частоте . Частота называется основной, колебание с частотой называется основным тоном, а колебания с частотами и т. д.- обертонами (соответственно первым, вторым и т. д.).
В струнных музыкальных инструментах колебания струн возбуждаются либо щипком или рывком пластинкой (гитара, мандолина), либо ударом молоточка (рояль), либо смычком (скрипка, виолончель). Струны совершают при этом не одно какое-нибудь из собственных колебаний, а сразу несколько. Одной из причин того, почему разные инструменты обладают различным тембром (§ 21), является как раз то, что обертоны, сопровождающие основное колебание струны, выражены у разных инструментов в неодинаковой степени. (Другие причины различия тембра связаны с устройством самого корпуса инструмента - его формой, размерами, жесткостью и т. п.)
Наличие целой совокупности собственных колебаний и соответствующей совокупности собственных частот свойственно всем упругим телам. Однако, в отличие от случая колебания струны, частоты обертонов, вообще говоря, не обязательно в целое число раз выше основной частоты.
На рис. 100 схематически показано, как колеблются при основном колебании и двух ближайших обертонах пластинка, зажатая в тиски, и камертон. Разумеется, на закрепленных местах всегда получаются узлы, а на свободных концах - наибольшие амплитуды. Чем выше обертон, тем больше число дополнительных узлов.
Рис. 100. Свободные колебания на частоте основного тона и двух первых обертонов: а) пластинки, зажатой в тиски; б) камертона
Говоря ранее об одной собственной частоте упругих колебаний тепа, мы имели в виду его основную частоту и попросту умалчивали о существовании более высоких собственных частот. Впрочем, когда речь шла о колебаниях груза на пружинке или о крутильных колебаниях диска на проволоке, т. е. об упругих колебаниях систем, у которых почти вся масса сосредоточена в одном месте (груз, диск), а деформации и упругие силы - в другом (пружина, проволока), то для такого выделения основной частоты имелись все основания. Дело в том, что в таких случаях частоты обертонов, начиная уже с первого, во много раз выше основной частоты, и поэтому в опытах с основным колебанием обертоны практически не проявляются.
Музыка есть таинственная арифметика души; она вычисляет, сама того не сознавая.
Г. Лейбниц
Ноябрьским утром 1717 г. на ступенях парижской церкви святого Жана ле Рона был найден младенец. Его взяли на воспитание и в честь святого церкви окрестили Жаном ле Роном. Мальчик рано проявил блестящий ум и жадную любознательность и вскоре стал гордостью всей Франции. Это был Жан ле Рон Д"Аламбер (1717-1783) - выдающийся французский математик, философ, писатель, член Парижской, Петербургской и других академий.
Круг интересов Д"Аламбера был необычайно широк: механика (принцип Д"Аламбера), гидродинамика (парадокс Д"Аламбера), математика (признак сходи мости Д"Аламбера), математическая физика (формула Д"Аламбера), философия теория музыки. Такой широты требовала и oабота вместе с Дени Дидро над созданием наменитой "Энциклопедии наук, искусств и ремесел", да и сам дух эпохи посвещения, когда к знаниям тянулись все, в том числе и "просвещенные деспоты" Фридрих II и Екатерина II. Последуя неоднократно приглашала Д"Аламбера быть воспитателем ее сына - цесаревича Павла, назначая при этом баснословное вознаграждение, но всегда получала деликатный, но твердый отказ.
Колебания струны длины l. Показаны два момента времени t 1
В 1747 г. Д"Аламбер опубликовал статью "Исследования по вопросам о кривой, которую образует натянутая струнa, приведенная в колебание", где впервые задача о колебании струны сводилась к решению дифференциального уравнения в частных производных. И хотя эта тема выходит за рамки школьной математики но ведь в знаниях "держать себя в рамках" - значит погубить свою любознательность!), мы рассмотрим простое и поистине красивое уравнение, описывающее колебание струны, так называемое полновое уравнение, с которого началась новая ветвь математики - математическая физика:
(10.1)
Здесь t - время; х - координата струны в положении равновесия; u = u(х, t) - неизвестная функция, выражающая отклонение точки с координатой х в момент времени t от положения равновесия; а 2 - коэффициент пропорциональности, характеризующий упругие свойства струны 
, T - сила натяжения струны, р - плотность однородной струны). Предполагается, что струна совершает малые колебания, происходящие в одной плоскости. Наконец, символы 
обозначают частную производную второго порядка, которая определяется как производная от производной 
. Частные производные - 
, как и обычная "школьная" производная характеризует скорость изменения функции u(х,t) по каждой из переменных х или t в отдельности при условии, что другая переменная не изменяется (у функций одной переменной y = y(x) - одна производная, а у функции двух переменных u = u(х,t) - две частные производные 
. Чтобы отличать частные производные от обыкновенных "школьных", пишут не прямую букву , а круглую .
Волновое уравнение (10.1) есть не что иное, как следствие второго закона Ньютона. Левая часть (10.1) выражает вертикальное ускорение струны в точке х, а правая часть - отнесенную к массе струны силу, вызывающую это ускорение, которая тем больше, чем больше вогнутость струны .
Д"Аламбер нашел общее решение уравнения (10.1)
которое содержит две произвольные функции φ(х,t) и ψ(х,t). Через пять лет Даниил Бернулли (1700-1782), математик, механик, физиолог и медик, почетный член Петербургской Академии наук, представитель славного рода Бернулли, который к настоящему времени подарил миру более 100 потомков, добившихся значительных результатов во всех сферах человеческой деятельности, и прежде всего в научной, получил другое общее решение уравнения (10.1)
Сравнивая решения Д"Аламбера (10.2) и Д. Бернулли (10.3), мы, казалось бы, приходим к абсурду: одно и то же уравнение (10.1) имеет совершенно непохожие решения! Но никакого абсурда здесь нет, так уж устроены дифференциальные уравнения. Они обладают бесчисленным множеством решений, что легко видеть из (10.2), где функции φ(x - at) и ψ(x + at) произвольные. При достаточно общих предположениях относительно функций φ и ψ правая часть (10.2) может быть представлена рядом (10.3).
Выбор того или иного частного решения дифференциального уравнения диктуется условиями, в которых протекает процесс (это так называемые граничные условия), и условиями, которые имели место в начале процесса (так называемые начальные условия). Только совокупность дифференциального уравнения, начальных и граничных условий определяет решение той или иной физической задачи. С помощью общего решения (10.2) Д"Аламбер решил одну из таких задач: найти колебания бесконечной струны (т. е. при отсутствии граничных условий), которой в начальный момент времени t = 0 придали некоторую форму f(х) и сообщили некоторое ускорение g(x). Математически задача ставилась так: найти решение уравнения (10.1), удовлетворяющее начальным условиям u(х,0) = f(x), u(х,0) = g(x), т. е. решить систему
(10.4)
Решение задачи (10.4) определяется формулой Д"Аламбера
Формула (10.5) в простейшем случае g(x) = 0, т. е. когда струну тихонько оттянули и отпустили, не придавая ей дополнительного ускорения, принимает вид
и физически означает, что сообщенный струне при t=0 профиль f(x) будет распространяться влево и вправо со скоростью а. Это так называемые две бегущие волны , движущиеся в противоположных направлениях с одинаковой скоростью а.
На самом деле бесконечных струн не бывает. Струна имеет конечную длину l и, как правило, жестко закреплена на концах. Так возникают граничные условия: u(0,t) = 0 - струна закреплена слева (х = 0); и (l,t) = 0 - струна закреплена справа (х = l). Ясно, что в этом случае бегущие волны будут отражаться от концов, взаимодействовать друг с другом и образовывать более сложную картину колебаний.
Задача о колебании конечной струны была независимо решена Д"Аламбером и Эйлером, а еще через полвека Жозеф Фурье изобрел новый метод, позволявший решать эту и многие другие задачи математической физики. Задача о колебании конечной струны формулируется так: найти решение волнового уравнения (10.1), удовлетворяющее начальным условиям u(х,0) = f(х), u t (x,0) = g(x) и граничным условиям u(0,t) = 0, u(l,t) = 0, т. е. решить систему
(10.6)
Жан Батист Жозеф Фурье (1768-1830) не был кабинетным ученым. Он взлетел на гребне Великой французской революции 1789 г. и из сына провинциального портного, готовившегося принять монашеский постриг, превратился в друга императора Наполеона. В 1798 г. Фурье участвовал в египетском походе Наполеона, где его жизнь не раз подвергалась опасностям. По возвращении из Египта Фурье занимался административной деятельностью, но находил время и для математических исследований. В 1807 г. он написал свою бессмертную работу "Математическая теория тепла". Главный математический результат Фурье можно описать так: при некоторых ограничениях всякую функцию f (х) можно представить в виде ряда (бесконечной суммы чисел или функций), называемого ныне рядом Фурье:
Фурье разработал метод решения уравнений типа (10.1), называемый методом разделения переменных Фурье.
Идея метода Фурье гениально проста. Решение уравнения (10.1) ищется в виде произведения двух функций X(х) и Т(t), каждая из которых зависит только от одной, "своей" переменной:
u(х,t) = X(x)T(t). (10.7)
Замена (10.7) расщепляет уравнение (10.1) на два дифференциальных уравнения в обыкновенных "школьных" производных:
(10.8)
где λ - неизвестный вспомогательный параметр. Решая уравнения (10.8) и удовлетворяя начальным и граничным условиям (10.6) (разумеется, мы опускаем все промежуточные выкладки, которых здесь, как и при выводе формулы Д"Аламбера (10.5), хватит на несколько страниц), находят окончательное решение задачи (10.6) о колебании конечной струны:
(10.9)
Выясним физический смысл решения (10.9), и прежде всего функций u n (х,t), составляющих это решение. Для этого выполним искусственное преобразование:
(Здесь мы воспользовались формулой синуса суммы двух аргументов и тем, что Таким образом, u n (х,t) можнс представить в виде
(10.10)
Из формулы (10.10) видно, что каждое решение u n представляет собой гармоническое колебание (т. е. колебание по закону синуса) с одной и той же частотой 
и фазой φ n . Амплитуда же колебаний А n (х) для разных точек струны разная, т. е. зависит от координаты точки струны х. Из (10.10) видно, что при х = 0 и х = l А n (0) = А n (1) = 0, т. е. на концах струна неподвижна.
Итак, во времени колебания струны происходят с постоянной частотой ω n , амплитуда колебания для каждой точки струны своя. При этом все точки струны одновременно достигают своего максимального отклонения в ту или другую сторону и одновременно проходят положения равновесия. Такие колебания называются стоячими волнами .
Пользуясь выражением для амплитуды стоячей волны (10.10) и учитывая, что 0≤x≤l, найдем неподвижные точки стоячих волн:
Неподвижные точки называются узлами стоячей волны. Ясно, что посередине между узлами расположены точки, в которых отклонения в стоячей волне достигают максимума. Эти точки называются пучностями стоячей волны.
Сделаем общий вывод: колебание конечной струны представляет собой бесконечную сумму стоячих волн u n (х,t), каждая из которых имеет постоянную частоту колебания 
и изменяющуюся по длине струны амплитуду В k-й стоячей волне имеется k
пучностей и (k + 1) узлов.
Перейдем теперь к "музыкальному содержанию" решения (10.9) и прежде всего к частотам колебаний. Мы пришли к выводу, что струна колеблется не только всей своей длиной, но одновременно и отдельными частями: половинками, третями, четвертями и т. д. Следовательно, струна издает звук не только основной частоты , но и призвуки частот . Тон основной частоты струны ω 1 называется основным тоном струны , а остальные тона, соответствующие частотам ω 2 , ω 3 , ..., ω k , ..., называются обертонами (верхними тонами) или гармониками . Основной тон струны принимается за первый обертон (первую гармонику). Именно обертоны, сливаясь в общем звучании с основным тоном, придают звуку музыкальную окраску, называемую тембром .
Различие тембров музыкальных звуков в основном объясняется составом и интенсивностью обертонов у разных источников звуков. Чем больше у звука обертонов, тем красивее, "богаче" он нам кажется. По тембру, т. е. по составу обертонов, мы отличаем звуки одной и той же высоты и одинаковой громкости, воспроизведенные на скрипке или фортепиано, голосом или на флейте. Разумеется, и сам инструмент способен давать различные тембровые окраски, что прежде всего относится к скрипке.
У скрипачей есть особый способ необычного по тембру звукоизвлечения - игра флажолетами. Слегка дотрагиваясь пальцем до струны в узлах стоячих волн, но так, чтобы струна не соприкасалась с грифом, скрипач гасит одни обертоны и оставляет другие. В результате возникает мягкий, немного свистящий звук, напоминающий по тембру звучание старинного Деревянного духового инструмента - флажолета. Например, дотронувшись до струны точно посередине, скрипач гасит все гармоники, имеющие в этой точке пучности, и сохраняет только гармоники, имеющие в этой точке узлы, т. е. четные гармоники. Таким образом, самой низкой частотой станет второй обертон 
.
Но это не будет по тембру звук точно на на октаву выше основного тона , так как он будет составлен только из четных гармоник. Аналогично, дотронувшись до струны в точке l/3, скрипач оставит только гармоники, кратные трем: ω 3 , ω 6 , ..., и получит флажолет, не похожий на первый, даже если сделать ω 2 = ω 3 . Игра флажолетами требует виртуозной точности. Ведь если мы не попадем точно в узел, то погасим вообще все гармоники и струна попросту не зазвучит!
Вот какую огромную роль играют в музыке слагаемые u n (х,t) в решении (10.9). Их с полным правом называют звуковой краской музыканта. Но не только музыканты, а и создатели музыкальных инструментов проявляют постоянную заботу об этих слагаемых, от которых зависит тембр звука. Достаточно напомнить об особом "итальянском тембре" скрипок работ знаменитых итальянских мастеров XVI-XVIII веков, представителей нескольких поколений семей Амати, Гварнери, Страдивари.
Из решения (10.9), задавая нужным образом функции f(х) и g(x) и вычисляя интегралы, можно формально получить законы, которые экспериментально обнаружил английский ученый-энциклопедист Томас Юнг (1773 - 1829):
1. Если возбуждать струну в какой-либо точке, то в этой точке возникает пучность и не может образоваться узел.
2. Если затормозить струну в какой-либо точке, то в этой точке возникает узел и не может образоваться пучность.
Из первого закона Юнга следует, что если возбуждать струну, например, точно посередине, то в ней погасятся все гармоники, имеющие в этой точке узел, т. е. все четные обертоны. Значит, мы потеряем половину обертонов и звук станет блеклым. Ясно, что чем дальше от середины мы будем возбуждать струну, тем меньше первых, самых важных гармоник мы потеряем. Тембр звука от этого станет полнее и ярче. Вот почему смычок на скрипке, правая рука на гитаре, молоточки на фортепиано - все они возбуждают струну приблизительно на 1/7-1/10 доли струны от места ее закрепления. Делается это для того, чтобы не потревожить первые обертоны, а значит, не обеднить музыкальный звук. Что касается игры на скрипке флажолетами, то она основана на втором законе Юнга, который является обратным к первому закону.
Прежде чем расстаться с законами Юнга, скажем несколько слов об их создателе. Томас Юнг был удивительным человеком. " Всякий может делать то, что делают другие" - таков был девиз его жизни. И Юнг необычайно преуспел в исполнении этого нелегкого правила. Он был цирковым актером (акробатом и канатоходцем), авторитетным знатоком живописи, играл практически на всех су. Шествовавших в его время музыкальных инструментах, занимался расшифровкой египетских иероглифов, знал массу языков, в том числе латинский, греческий и арабский. И кроме всех этих "увлечений", Юнг получил блестящие результаты в науках: физике (волновая теория света), теории упругости (модуль упругости Юнга), оптике, акустике, астрономии, физиологии, медицине. Юнг написал около 60 глав научных приложений к знаменитой "Британской энциклопедии".
Рассмотрим подробнее основной тон струны. Вспоминая, что 
, получим формулу для частоты основного тона:
(10.11)
откуда легко увидеть законы колебания струны, которые экспериментально обнаружили еще древние греки и которые затем переоткрыл и описал в своей "Универсальной гармонии" Марен Мерсенн:
1. Для струн одинаковой плотности и одинакового натяжения частота колебания обратно пропорциональна длине струны (это не что иное, как "первый закон Пифагора - Архита"; см. с. 101).
2. При заданной длине и плотности струны ее частота пропорциональна корню квадратному из натяжения.
3. При заданной длине и натяжении частота струны обратно пропорциональна корню квадратному из ее плотности. (При постоянной плотности чем толще струна, тем меньше частота ее колебаний, т. е. тем ниже звук.)
Разумеется, все эти законы (по крайней мере, качественно) можно было установить на монохорде.
Но обратимся вновь к обертонам. Легко видеть, что частоты обертонов относятся как числа натурального ряда:
Таким образом, струна издает целый звукоряд тонов, называемый натуральным звукорядом. Теоретически натуральный звукоряд бесконечен. На практике же имеют значение первые 16 обертонов, так как остальные обертоны слишком мало отличаются друг от друга, обладают слишком малой энергией и фактически не слышны.
Натуральный звукоряд. Полагая ω 1 = l, частоты натурального звукоряда выражаются натуральным рядом чисел (ω n = n). Натуральный звукоряд содержит все консонансы и все интервалы чистого строя
В самом деле, из (10.12) следует, что интервальный коэффициент двух соседних гармоник ω n и ω n+1 равен 
(n = 1, 2, 3, ...). Поскольку 
то мы легко приходим к выводу: с ростом номера п интервал между соседними гармониками натурального звукоряда уменьшается и в пределе стремится к чистой приме (унисону).
На рисунке показаны первые 16 гармоник колеблющейся струны, образующие натуральный звукоряд. Цифры справа обозначают частоты гармоник, считая ω 1 = 1, а красная линия (гипербола) отсекает часть струны 1/n, которая колеблется с частотой ω n = n. Мы видим, что второй обертон и основной тон составляют интервал октавы ω 2 /ω 1 = 2. Третий и второй обертоны - интервал квинты: ω 3 /ω 2 = 3/2. Четвертый и третий - кварты: ω 4 /ω 3 = 4/3. Пятый и четвертый - большой терции: ω 5 /ω 4 = 5/4. Шестой и пятый - малой терции: ω 6 /ω 5 = 6/5. Но ведь это есть не что иное, как набор совершенных и несовершенных консонансов! Таким образом, мы пришли к разгадке "закона консонансов" - "второго закона Пифагора - Архита" (с. 101 - 102): консонантные интервалы, которые математически выражаются отношением
вида (n = 1, 2, 3, 4, 5), определены самой природой колебания струны! Все консонансы заключены в первых шести гармониках, т. е. первых шести тонах натурального звукоряда, причем по мере удаления от первой гармоники (основного тона) степень консонантности интервала убывает. Итак, закон целочисленных отношений для консонантных интервалов , который, по преданию, был экспериментально открыт Пифагором на монохорде, является следствием математического решения задачи о колебании струны и непосредственно вытекает из решения (10.9).
Переходя к более высоким гармоникам, нетрудно обнаружить также два интервала тона чистого строя: ω 9 /ω 8 = 9/8, ω 10 /ω 9 = 10/9 и интервал полутона чистого строя: ω 16 /ω 15 = 16/15. Таким образом, все интервалы чистого строя содержатся в натуральном звукоряде ! Вот почему чистый строй более приятен в гармоническом звучании, чем пифагоров строй.
Но и сами тона чистого строя (8.7) почти полностью определены натуральным звукорядом. В самом деле, если рассмотреть октаву между 8-й и 16-й гармониками, принимая частоту 8-й гармоники за единицу (т. е. поделив все частоты на 8), то мы обнаружим в этой октаве все ступени чистого строя, кроме 4-й (4/3) и 6-й (5/3). Следовательно, чистый строй почти целиком содержится в натуральном звукоряде .
Однако это коварное "почти" до сих пор составляет одну из загадок музыки. В самом деле, почему именно 7, 11 и 13-й обертоны (14-й обертон является октавным повторением 7-го) не входят ни в один из музыкальных строев? Знаменитый "фальшивый" 7-й обертон третье столетие не дает покоя теоретикам музыки! С одной стороны, ясно, что неправильно называть этот звук фальшивым, ибо он дан самой природой, которую трудно упрекнуть в фальши. Но с другой стороны, все теоретики музыки, начиная с Рамо, были слишком большими музыкантами, чтобы включить седьмую гармонику в какую-либо музыкальную систему (седьмой звук явно "резал ухо"!). Впрочем, еще в XVIII веке французский музыкальный теоретик Балльер с присущей французу легкостью писал: "Разница между древностью и современностью заключается в том, что тогда начинали считать диссонансы с 5-го призвука, а теперь начинают их считать лишь с 7-го". Не пойдет ли развитие музыки так, что в новых музыкальных системах найдется место и 7, и 11, и 13-му обертонам?.. А пока молоточки фортепиано, следуя первому закону Юнга, ударяют на 1/8 длины струны, чтобы максимально снизить силу злополучного 7-го обертона.
Наконец, отметим еще одну важную особенность натурального звукоряда. Глядя на рисунок, мы видим, что 4, 5 и 6-я гармоники образуют мажорное звучание (до-ми-соль ). А если к ним добавить еще и 1-ю, и 2-ю гармоники, то получится мажорное трезвучие в сопровождении октавного баса! Итак, мажорное трезвучие составлено из ближайших гармоник (4, 5 и 6-й) основного тона (баса мажорного трезвучия) . Следовательно, оно не только консонирует, но и обладает акустическим единством, заложенным в самой природе колебания струны. Это дало основание одному из последних универсальных ученых - немецкому математику, физику, физиологу и психологу Герману Гельмгольцу (1821 - 1894) утверждать, что "мажорный аккорд наиболее натурален из всех аккордов".
Ну а минорное трезвучие? Споры о природе минора не затихают и по сей день. В них участвовали Рамо, Д"Аламбер, Руссо, Гёте, Гельмгольц, многие наши современники. На сегодня мнения сходятся в том, что поскольку в минорном трезвучии (до - ми-бемоль - соль) второй звук (ми-бемоль) лежит на полутон ниже пятой гармоники основного тона, то он образует с ней едва слышимый диссонанс, который и обусловливает некоторую "затененность", "нечто мрачное и неясное, необъяснимое для слушателя" (Гельмгольц). По o этой причине в музыке Баха, Генделя, Моцарта минорные произведения часто заканчиваются мажорным - наиболее натуральным, просветленным - аккордом.
Итак, в мажорной гамме третья ступень как бы тяготеет вверх, тогда как в минорной она тяготеет вниз. Движение же вверх воспринимается нами как восхождение к свету, просветление, радость. Напротив, движение вниз ассоциируется со спуском в темноту, затемнением, печалью. Эти объективные предпосылки поддерживаются, кроме того, определенной традицией применения мажора и минора. В тех же случаях, когда эти традиции нарушаются, мы встречаем разудалую песню "Яблочко", написанную в миноре, и молитву "Ave Maria ", которую, несмотря на ее название - "Радуйся, Мария" - и мажорный лад, никак не назовешь веселой. К сожалению, смешивание объективных физико-математических законов строения мажора и минора с их субъективной эстетической оценкой породило вокруг них много ненужных споров.
В заключение остановимся еще на одной проблеме колеблющейся струны. До сих пор, следуя решению (10.9), мы пытались "разъять, как труп" колебания струны на простейшие гармонические составляющие. Но ведь на самом деле, опять же согласно (10.9), составляющие колебание струны гармоники складываются, образуя сложную картину колебаний. Характер этой картины зависит прежде всего от амплитуд гармоник. Решить эту задачу в общем виде не просто, поэтому остановимся на более простой задаче.
Пусть складываются два колебания постоянной и одинаковой амплитуды, равной для простоты единице, и разных частот ω 1
Суммарное колебание, пользуясь формулами суммы синусов и косинуса половинного угла, представим в виде
При сложении двух колебаний, близких по частоте (ω 1 = 8 и ω 2 = 10), возникают биения - периодическое усиление и ослабление звука, происходящее с частотой биений ω = ω 2 - ω 1 = 2
Равенство (10.13), когда частоты ω 1 и ω 2 близки друг к другу с достаточной степенью точности, можно трактовать следующим образом: сумма двух гармонических колебаний частот ω 1 и ω 2 является "почти гармоническим" колебанием, частота которого есть среднее арифметическое данных частот 
, а амплитуда изменяется во времени с частотой ω 2 -ω 1 и ограничена сверху функцией , а снизу - функцией - . Легко видеть, что амплитуда суммарного колебания пульсирует с частотой ω 2 -ω 1 от нуля до максимального значения и затем снова до нуля. По этой причине такие колебания называют биениями
. Из (10.13) также видно, что максимальная амплитуда биений вдвое больше амплитуд составляющих колебаний.
Итак, при сложении двух близких по частоте колебаний возникают биения" т. е. почти гармонические колебания с частотой, равной средней частоте данных колебаний, и амплитудой, пульсирующей с частотой биений, которая равна разности частот данных колебаний. Издаваемый при биениях звук то периодически усиливается, то замирает.
Перейдем к музыкальной стороне явления биений. Известно, что всякое прерывистое раздражение нервов воспринимается сильнее, чем постоянное. Однако с увеличением частоты раздражений нерв не успевает следить за изменениями, отдельные раздражения сливаются между собой и становятся незаметными. Экспериментально установлено, что наиболее отчетливо слышны биения с частотой 4-5 Гц (колебаний в секунду). Биения с частотой около 15 Гц еще различимы, а при частоте около 30 Гц они начинают сливаться, но создают неприятное ощущение хрипловатости звучания.
Существует теория Гельмгольца, которая объясняет явления консонанса и диссонанса биениями, возникающими между гармониками двух звучащих основных тонов. Согласно теории Гельмгольца, от наличия биений, их частоты и громкости (амплитуды) зависит степень консонантности и диссонантности интервала. Поясним эту теорию на примере. В таблице 2 в качестве основного тона взяты нота до малой октавы, частота которой равна 131 Гц, и ее пять обертонов. Далее приведены первые пять обертонов для звуков до 1 , соль, фа, ми (чистого строя), ми (пифагорова строя) и до-диез (чистого строя), которые образуют с основным тоном до соответственно интервалы октавы, квинты, кварты, большой терции, пифагоровой терции и малой секунды.
Понятно, что для октавы совпадают частоты гармоник, номера которых относятся как 2/1, для квинты - как 3/2 и т. д. (см. табл. 2). Сравнивая частоты первых гармоник, мы видим, что чем меньше становится интервал, тем ближе частоты основных тонов, тем различимее будут биения и, следовательно, тем меньше будет степень консонантности интервала. Поэтому самым консонантным интервалом является октава, затем идут квинта и кварта. Все три этих интервала не дают биений и относятся к совершенным консонансам. Терция дает в первых гармониках чуть более 30 биений, т. е. на пороге различимости, и поэтому относится к несовершенным консонансам. А вот малая секунда дает 9 биений (140-131 = 9) и поэтому является явным диссонансом. Заметим, что четвертая гармоника пифагоровой терции (663,2) и пятая гармоника основного тона (655) дают 8 биений (663-655 = 8). Эти биения и создают неприятное гармоническое звучание пифагоровой терции. Однако поскольку они происходят в старших гармониках, т. е. значительно слабее биений в первых гармониках, то ясно, что пифагорову терцию нельзя причислить к диссонансу наравне с малой секундой, где такие же биения происходят в первых гармониках.
Таким образом, мы выполнили обещание, данное на с. 130 и объяснили, почему пифагорова терция в гармоническом исполнении звучит напряженно по сравнению с чистой. Конечно, теория Гельмгольца не решает всех музыкальных загадок колеблющейся струны - таких как проблема 7-го обертона, например,- и здесь еще остается немало точек приложения для пытливого ума.
Не правда ли, какое удивительное разнообразие законов, свойств и загадок таит в себе простое колебание простой струны! Законы Пифагора - Архита (особенно "закон консонансов"), законы Мерсенна и законы Юнга, решения Д"Аламбера Д. Бернулли и Фурье, натуральный звукоряд и мажорное трезвучие, биения... Вот уже третье тысячелетие обыкновенная струна открывает человечеству свои необыкновенные тайны! И быть может, кто-то задумается следующий раз об этих тайнах, прежде чем ударить по струнам старенькой гитары.
ВЫ НЕ ПОВЕРИТЕ, что вытворяет ваша струна!В этом посте я попробую изложить 3 взаимосвязанные темы: как происходят колебания гитарной струны, как работают флажолеты и почему звук электрогитарного датчика меняется в зависимости от его местоположения относительно струны.
Я сделал для примеров несколько видео со спектрограммами. Это простая штука. По горизонтали время, по вертикали частота, яркость линии означает интенсивность частот. Спектрограмма многое говорит о звуке.
Все музыкальные ноты выглядят на спектрограмме как ряд параллельных линий:
Видео 1: спектрограмма мелодии, сыгранной на электрогитаре
Всё потому, что любое сложное периодическое колебание (а значит - любая музыкальная нота) состоит из ряда колебаний кратных частот или может быть представлено в виде такой суммы. Они называются гармониками - первая, вторая, третья и так далее. Частота второй гармоники в два раза выше, чем у первой, третей гармоники - втрое выше, чем у первой, и так далее. Так что спектр ноты с частотой 100 Гц состоит из частоты 100 Гц и кратных ей частот. У гитарной струны может быть от нескольких до нескольких десятков гармоник. Точное их количество назвать затруднительно - как правило, чем выше гармоника, тем она слабее и тем быстрее затухает. Поэтому я буду описывать эти ряды вот так: {100, 200, 300, 400, 500, ...} Гц. В ряду может недоставать каких-то гармоник (присмотритесь к видео 1), что не мешает ноте быть нотой.
Когда пишут что «нота имеет такую-то частоту» , имеется в виду именно частота первой гармоники.
«Расклад» гармоник по уровням может быть разным - одни сильнее, другие слабее. От этого зависит тембр звука: много верхних гармоник - звук яркий, пронзительный, мало - звук мягкий, глухой. Вот одна нота (Ля 110 Гц) на разных инструментах:
Видео 2: нота Ля (110 Гц), сыгранная разными инструментами
Движения
Для примера возьмём открытую пятую струну Ля. Частота её первой гармоники - 110 Гц.
Почему именно пятую? Вот частоты всех открытых струн в стандартном строе:E: примерно 329,63 Гц
B: примерно 246,94 Гц
G: примерно 196 Гц
D: примерно 146.83 Гц
A: ровно 110 Гц
E: примерно 82.4 ГцПонятно, почему пятую.
Важный момент: в этом посте говоря о «струне», о «длине струны», о картине колебаний и т.д., я буду иметь в виду именно ту часть струны, которая вибрирует - от порожка до бриджа или от лада до бриджа, если струна прижата. Не буду каждый раз это обговаривать.
Струна одновременно совершает множество разных видов колебаний.
Первое колебание - самое простое:
Колебание первой гармоники струны (по клику откроется анимированная картинка)
Струна колеблется одной «дугой», с частотой первой гармоники (в нашем примере - 110 Гц). В центре струны амплитуда колебания больше всего, а чем ближе к краям, тем оно слабее.
Может показаться, что вот так то струна и колеблется, но это лишь часть картины.
Второе колебание:
Колебание второй гармоники струны (кликабельно)
Струна колеблется как бы отдельными половинками, в противоположных направлениях. Половинка колеблется вдвое чаще, чем целая струна, поэтому у второго колебания частота вдвое выше, чем у первого. В нашем случае получается частота второй гармоники - 220 Гц.
В середине каждой из «половинок» колебание максимально. Чем ближе к краям или середине струны, тем колебание слабее. В середине струны получается любопытная штука - так называемый узел колебания . Это место, расположенное как раз между половинками, в котором колебание второй гармоники отсутствует. Здесь могут быть другие колебания, но второй гармоники тут точно не будет.
Третье колебание:
Колебание третьей гармоники струны (кликабельно)
Здесь струна колеблется уже «третями» - внешние трети идут в одном направлении, средняя в обратном. А частота этого колебания втрое выше, чем у первой гармоники (в нашем случае - 330 Гц). Здесь уже два узла колебания - в точках, делящих струну на три равные части.
Остальные колебания устроены по тому же принципу. Чем дальше, тем больше частота колебания, количество частей и «узлов» между ними:
Амплитуда колебаний первых десяти гармоник струны в разных её участках
Подытожим: в разных точках струны происходят разные картины колебаний, с различными соотношениями гармоник. Например, в середине струны вторая гармоника отсутствует, а первой или третьей тут полно. Например, если взять точку струны совсем рядом с краем струны, то первой гармоники там будет мало, а четвёртой - заметно больше, чем первой. И у каждой гармоники своё «распределение по струне».
Флажолеты
Посмотрим теперь на самый простой натуральный флажолет: прикасаемся к струне пальцем левой руки над 12 ладом, а правой рукой дёргаем струну и получаем ноту на октаву выше.
Что за магия? Как так получается? Сейчас разберёмся.
Вернёмся опять к пятой струне с рядом гармоник {110, 220, 330, 440, 550, ...} герц.
Когда струну просто дёргают, в её колебании есть все возможные гармоники. А вот при извлечении флажолета палец, который прикоснулся к струне, убирает часть гармоник. Если палец находится над узлом колебания какой-то гармоники, он не мешает этому колебанию (примерно так). В остальных случаях - мешает, и колебание гаснет.
В нашем примере палец находится на середине струны: в этом месте у всех чётных гармоник находится узел колебания, а у всех нечётных - максимум колебания. Поэтому палец оставляет только чётные гармоники, а все нечётные «вырубает». И струна, вместо того, чтобы выдать свой полный ряд гармоник {110, 220, 330, 440, 550, ...} герц, теперь выдаёт ряд {220, 440, 660, 880, 1100, ...} герц. А значит, вместо ноты с частотой 110 Гц теперь звучит нота с частотой 220 Гц (гармоники - частота 220 Гц и кратные ей). А это - нота на октаву выше.
Повышение частоты ноты в 2 раза всегда делает эту ноту на октаву выше. Например, нота с частотой 220 Гц на октаву выше ноты с частотой 110 Гц.
Соотношение частот 3:2 даёт квинту. Например, нота с частотой 660 Гц на квинту выше ноты с частотой 440 Гц.
Соотношение 4:3 - даёт кварту.
Соотношение 5:4 - большую терцию.
Соотношение 6:5 - малую терцию.
На самом деле всё немножко сложнее, но об этом - в другой раз.
Палец, стоящий над 7-м или 19-м ладом, находится над узлом колебания третьей гармоники. Поэтому он глушит всё кроме третьей гармоники и кратных ей (3-я, 6-я, 9-я,..). Частота ноты от такого флажолета увеличится в 3 раза и вместо ноты на открытой струне получится нота на октаву+квинту выше её.
Палец над 5-м или 24-м ладом оставляет только четвёртую гармонику и кратные ей и повышает частоту ноты в 4 раза (плюс 2 октавы).
Палец над 4-м ладом, 9-м или 16-м ладом оказывается над узлом пятой гармоники и повышает частоту ноты в 5 раз (плюс 2 октавы и большая терция).
Видео 3: Флажолеты на открытой третьей струне в сравнении с обычной открытой струной. 12-й лад, 7-й, 5-й, и 4-й
У искусственных флажолетов (классический двухпальцевый, рокерский медиаторный, или тэповый флажолет) техника исполнения другая, но принцип действия тот же: мы заставляем струну колебаться и в то же время запрещаем ей колебаться в какой-то конкретной точке, «выключая» таким образом часть гармоник.
Один нюанс: искусственные флажолеты обычно играются на прижатых струнах. А у прижатой струны точки, где нужно делать флажолеты, сдвигаются. Например, если прижать ноту на 2 ладу, все флажолетные точки сдвинутся на 2 лада ближе к бриджу: середина струны теперь на 14-м ладу, точки, которые делят струну на трети - на 9-м или 21-м, и так далее.
Звукосниматель и струна
Теперь вернёмся от флажолетов к обычному звукоизвлечению и посмотрим, что происходит при съёме струны звукоснимателем.
У каждой гармоники амплитуда колебания варьируется в зависимости от того, какую точку струны мы рассматриваем. Эта зависимость у разных гармоник разная, так что в каждой точке струны своя картина гармоник. Магнитный звукосниматель электрогитары или баса снимает колебания не всей струны, а только её небольшой части, которая находится под ним. Попробуем разобраться, как зависит картина колебаний от того, какую точку струны мы снимаем.
Если звукосниматель стоит над узлом колебаний какой-то гармоники, то он её не снимет. Если рядом с узлом - снимет, но слабо. Чем дальше от узлов, тем больше этой гармоники попадёт в звукосниматель.
Если у вас под рукой есть стратокастер, можно проделать простой эксперимент: воткнуться в комбик, или во что угодно, главное - на чистом звуке, никакого подгруза. Переключиться на бриджевый звучок. Взять на любой струне открытый флажолет на 5-м ладу. Переключиться на нэковый звучок. Взять такой же флажолет. Разница будет радикальной - во втором случае звука практически нет.А всё потому, что нэковый звукосниматель на стратокастере расположен практически на 1/4 длины открытой струны. Поэтому 4-ю гармонику открытой струны (и кратные ей) он практически не улавливает. А извлекая открытый флажолет на 5-м ладу, мы как раз оставляем только эти гармоники.
Допустим, звукосниматель стоит ровно под серединой струны (серая линия на картинке ниже). В этом месте у всех нечётных гармоник максимум колебания, а у всех чётных - «узел». Поэтому на выходе этого звукоснимателя будут только нечётные гармоники, а чётных не будет. Например, если взять всё ту же струну Ля, то вместо ряда {110, 220, 330, 440, 550, ...} Гц датчик выдаст ряд {110, 330, 550, 770, 990, ...} Гц. Заметим, в отличие от флажолетов это не даст другую ноту - у нас все гармоники по прежнему кратны 110 герцам, а не чему-то другому.
Теперь более реалистичный пример. Возьмём три звукоснимателя:
«нэковый» - на расстоянии 1/4 длины струны от бриджа,
«бриджевый» - на 1/20 длины струны от бриджа,
и «средний» - между ними, примерно на 1/7 длины струны от бриджа
(приблизительно так расположены три сингла на стратокастере)...
И посмотрим, какие гармоники открытой струны и в каких количествах в эти датчики попадут.
Например, из картинки выше понятно, что «нэковый» звукосниматель (синяя линия) не будет «слышать» четвёртую гармонику (а так же восьмую и все остальные гармоники, кратные четвёртой). Вторую, шестую и десятую он «услышит» максимально. Первую - процентов на 70. И так далее. Пройдёмся по всем 10 гармоникам во всех четырёх положениях и увидим такие картины гармоник:
Амплитуда колебаний первых десяти гармоник струны в четырёх точках (по клику откроется в полном размере)
Уже видно, почему нэковый датчик звучит «глубже» бриджевого - он получает гораздо больше нижних гармоник.
Обнаружилось интересное: звукосниматель работает как фильтр - в каждом случае имеется характерный ряд провалов в картине гармоник. Чем ближе к бриджу, тем эти провалы выше и реже (у «красного датчика» первый провал придётся на 20-ю гармонику). Если датчик стоит над узлом какой-то гармоники - он полностью теряет эту гармонику и все кратные ей. Если нет - провал попадёт куда-то между гармониками, как у нашего «зелёного датчика». Положение провала относительно гармоник изменяется РОВНО во столько же раз, во сколько датчик стал ближе или дальше от бриджа.
С открытой струной мы разобрались. Когда мы прижимаем струну на любом ладу, её вибрирующая часть укорачивается и вся картина колебаний сжимается по направлению к бриджу - все точки и участки (максимумы, узлы гармоник и всё остальное) сдвигаются на новое место. Звукосниматель, конечно же, остался там же где и был, поэтому теперь он «слышит» другую картину гармоник.
И частоты этих гармоник тоже получатся другие - ведь струну укоротили и увеличили этим частоту её колебаний. Поэтому происходят две штуки:
1. Вся картина колебаний струны «ужимается»: все точки (середина, треть струны и так далее) сдвигаются и становятся в N раз ближе к бриджу. Так как звукосниматель никуда не двигался, то его положение относительно струны теперь в N раз «дальше» от бриджа. А от этого положение «провалов» относительно гармоник понижается в N раз.
2. Частота колебания струны и частоты всех гармоник становятся выше в ТЕ ЖЕ N раз.
Эти два явления полностью уравновешивают друг друга - во сколько раз увеличивается частота гармоник, во столько же падает положение «провалов» относительно гармоник. В итоге частоты «провалов» в герцах у нашей струны не меняются!
Я это подробно расписывать не буду, только проиллюстрирую «на пальцах».Рассмотрим «синий» звукосниматель, стоящий в 1/4 длины струны от бриджа. Берём открытую пятую струну. Она издаёт колебания с частотами {110, 220, 330, 440, 550, ...} Гц, а звучок из-за своего расположения «проваливает» 4-ю гармонику и кратные ей - то есть, частоты 440, 880, 1320 Гц и т.д.
Прижмём эту же струну на 12 ладу. Теперь струна колеблется с частотами {220, 440, 660, 880, 1100, ...} Гц, а звукосниматель находится на её середине и «теряет» все чётные гармоники - то есть всё те же 440, 880, 1320 Гц и т.д. Теперь это не каждая четвёртая, а каждая вторая гармоника, но частоты то те же.
Это легко проверить: подключаем гитару, включаем спектроанализатор, выбираем один из звукоснимателей и делаем слайд по всей струне. Будут видны характерные частотные провалы, которые НЕ ЗАВИСЯТ от того, на каком ладу нота:
Видео 4: частотные провалы на одной и той же струне, снятой сначала бриджевым, потом нэковым синглом.
Чем ближе к бриджу расположен звукосниматель, тем провалы реже и выше.
Положение «провалов» зависит только от двух вещей:
1. Частота колебания открытой струны.
2. Положение звукоснимателя относительно струны.
Поэтому «фильтр» на каждой струне будет свой - чем выше настроена струна, тем провалы выше и реже. Это хорошо видно при игре чистых переборов, например:
Видео 4: частотные провалы всех шести струнах, снятых нэковым синглом. Аккордовый перебор, снятый им же.
Основная причина, по которой различается звук датчиков, расположенных под разными участками струны - это «фильтр», который получается из-за того, что гармоники определённым образом распределены по струне. Этот фильтр существует всегда, где бы ни находился датчик. Структура его одинакова, меняется лишь масштаб.
Одно из следствий всего этого - чем ближе к бриджу, тем больше изменение положения звукоснимателя сказывается на звуке. Если сдвинуть нэковый звукосниматель на пару сантиметров в сторону - частоты «фильтра» сместятся на несколько процентов. Если на столько же сдвинуть бриджевый датчик - частоты сдвинутся на несколько десятков процентов. Потому что вопрос не в том, насколько сдвинулся датчик, а во сколько раз он ближе/дальше к бриджу. Надо воспринимать всё логарифмически.
В частности, иногда встаёт вопрос - какую из катушек оставлять рабочей при отсечке хамбакера? Так вот у нэкового хамбакера разница между катушками получится совсем небольшая, а у бриджевого - радикальная.
Недавно вконтакте
59.Стоячие волны. Колебания струны.
Стоя́чая волна́ - колебания в распределенных колебательных системах с характерным расположением чередующихся максимумов (пучностей) и минимумов (узлов) амплитуды. Практически такая волна возникает при отражениях от преград и неоднородностей в результате наложения отражённой волны на падающую. При этом крайне важное значение имеет частота, фаза и коэффициент затухания волны в месте отражения.
Примерами стоячей волны могут служить колебания струны, колебания воздуха в органной трубе; в природе - волны Шумана.
Чисто стоячая волна, строго говоря, может существовать только при отсутствии потерь в среде и полном отражении волн от границы. Обычно, кроме стоячих волн, в среде присутствуют и бегущие волны, подводящие энергию к местам её поглощения или излучения.
Для демонстрации стоячих волн в газе используют трубу Рубенса.
Уравнение колебаний струны относится к уравнениям гиперболического типа.
Каждую точку струны можно охарактеризовать значением ее абсциссы x. Для определения положения струны в момент времени t достаточно знать компоненты вектора смещения точки xв момент времени t.
Будем предполагать, что смещения струны лежат в одной плоскости (x,U) и что вектор смещения
перпендикулярен в любой момент времени к оси x; тогда процесс колебания можно описать одной функцией U(x,t) (смотри рисунок) .
Функция U(x,t) характеризует вертикальное перемещение струны.
Уравнение колебаний струны.
а=const- зависит от упругости, жесткости, массы и т. д.
Существуют следующие методы решения уравнения колебаний струны
Метод Даламбера (метод бегущих волн, метод характеристик);
Метод Фурье (метод стоячих волн, метод разделения переменных).
60. Громкость и высота тона звука.
Звуковые волны – продольные.
сейсмические – поперечные и продольные
20 – 20000 Гц > …..
инфра ультра
звук звук
Тон – звук одной частоты.
Обертон – дополнительная частота.
Тембр – оттенок звука.
Шум – много частот.
Громкость звука зависит от амплитуды колебаний.
Высота звука зависит от частоты колебаний.
61. Эффект Доплера.
Эффе́кт До́плера - изменение частоты и длины волн, регистрируемых приёмником, вызванное движением их источника и/или движением приёмника. Его легко наблюдать на практике, когда мимо наблюдателя проезжает машина с включённой сиреной. Предположим, сирена выдаёт какой-то определённый тон, и он не меняется. Когда машина не движется относительно наблюдателя, тогда он слышит именно тот тон, который издаёт сирена. Но если машина будет приближаться к наблюдателю, то частота звуковых волн увеличится (а длина уменьшится), и наблюдатель услышит более высокий тон, чем на самом деле издаёт сирена. В тот момент, когда машина будет проезжать мимо наблюдателя, тот услышит тот самый тон, который на самом деле издаёт сирена. А когда машина проедет дальше и будет уже отдаляться, а не приближаться, то наблюдатель услышит более низкий тон, вследствие меньшей частоты (и, соответственно, большей длины) звуковых волн.
Для волн, распространяющихся в какой-либо среде (например, звука) нужно принимать во внимание движение как источника так и приёмника волн относительно этой среды. Для электромагнитных волн (например, света), для распространения которых не нужна никакая среда, имеет значение только относительное движение источника и приёмника.
Эффект был впервые описан Кристианом Доплером в 1842 году.
Также важен случай, когда в среде движется заряженная частица с релятивистской скоростью. В этом случае в лабораторной системе регистрируется черенковское излучение, имеющее непосредственное отношение к эффекту Доплера.
Источник волн перемещается налево. Тогда слева частота волн становится выше (больше), а справа - ниже (меньше), другими словами, если источник волн догоняет испускаемые им волны, то длина волны уменьшается. Если удаляется - длина волны увеличивается.
| " |
Цель работы : изучение волновых явлений, условия существования стоячих волн, исследование упругих свойств струны.
Основные теоретические положения
Пусть точка, совершающая колебания, находится в среде, все частицы которой связаны между собой. Тогда энергия колебаний точки может передаваться окружающим точкам, вызывая их колебания. Явление распространения колебаний в среде называется волной. При этом колеблющиеся частицы не перемещаются с распространяющимся колебательным процессом, а колеблются около своих положений равновесия.
Если в неограниченной среде беспрепятственно распространяется единственная волна, то она называется бегущей. Составим уравнение бегущей волны, позволяющее определять смещение любой точки волны в любой момент времени.
Р
Рис. 9.1. К выводу
уравнения бегущей волны
t
’.
Найдём смещение элементов
струны, как функцию координаты x
и времени
t
,
то есть функцию
.
Очевидно, что для точкиx
=0,
=
D
(t
’)=
Asin
t
’
(рис. 9.1). Предположим, что
бегущее по струне в
озмущение
распространяется с некоторой скоростью
.
Смещение элемента струныx
в момент t
равно смещению элемента x
=0
в момент t
’
=
,
если расстояние между ними равно
расстоянию, которое возмущение проходит
за время t
-
t
’
со скоростью
.
Тогда точкиx
=0
и x
=
x
колеблются в одной фазе:
x
=
(t
-
t
’),
,
.
Поэтому уравнение бегущей синусоидальной
волны
=
=
Asin
t
’
,
то есть
.
(9.1)
Преобразуем
функцию (9.1):
.
Обозначим
=
k
и назовём его волновым числом, тогда
=
.
Следовательно, скорость
,
.
Величину
,
равную расстоянию, которое возмущение
преодолевает за период колебаний,
назовём длиной волны, то есть
,
тогда
,
.
Уравнение (9.1) и есть уравнение бегущей одномерной (или плоской) волны. При заданном x оно позволяет определить положение точки (с координатой равновесного положения x ) в любой момент времени t . При заданном t оно позволяет определить мгновенные положения всех колеблющихся точек.
Таким образом, видим, что в волновом движении имеет место двоякая периодичность. С одной стороны, каждая частица среды совершает периодическое движение во времени, с другой стороны, в каждый момент времени все частицы располагаются на линии, форма которой периодически повторяется в пространстве.
О
пределим
скорость распространения продольных
колебаний вдоль бесконечно
длинного стержня с постоянным поперечным
сечением.
П
Рис. 9.2.
Распространение упругой деформации
вдоль стержня
(рис.
9.2) вблизи
этого сечения происходит уплотнение
материала стержня, и возникает деформация
сжатия. Появляются упругие силы,
стремящиеся восстановить первоначальную
плотность, в результате чего возникает
сжатие соседних областей и таким образом
локальное возмущение плотности вблизи
левого края стержня распространяется
вправо со скоростью
.
Импульс
силы упругости
равен
.
Если Е −
модуль сжатия,
иначе называемый модулем
Юнга, то
.
За время
деформация
распространяется на
расстояние
.
Масса участкастержня,
охваченная деформацией, увеличится
на
вследствие
увеличения
плотности материала на
.Так как 
,то
.
В соответствии со вторым зaконом
Ньютона импульс силы упругости равен
изменению импульса, то есть
.
Подставляя все величины, получим
или 
,
(9.2)
где
- погодная плотность материала стержня.
Уравнение
(9.1)
описывает
волну, распространяющуюся в положительном
направлении оси ох.
При
изменении направления распространения
волны на
противоположное второе слагаемое в
аргументе косинуса изменяет знак, так
как
заменяется
на
.
(9.3)
Рассмотрим теперь распространение волны в струне, закрепленной с обеих сторон. При этом волна, движущаяся в одном направлении, достигнув второго закрепленного конца струны, отразится и станет распространяться в противоположном направлении. Таким образом вдоль длины струны возникнет явление наложения волн, распространяющихся в противоположных направлениях. Если свойства среды не изменяются под воздействием распространяющейся волны, то будет выполняться принцип суперпозиции, согласно которому каждая волна распространяется в среде независимо от других. В этом случае результирующее смещение z частиц среды будет определяться как сумма смещений z 1 и z 2 , обусловленных прохождением отдельных волн. В результате будет наблюдаться в различных точках среды усиление или ослабление колебаний в зависимости от фаз приходящих возмущений.
Сложение волн, при котором в разных точках среды образуются усиления и ослабления амплитуды колебаний, называется интерференцией волн. Такая интерференционная картина сохраняется во времени.
Рассмотрим интерференцию двух волн с одинаковой амплитудой, распространяющихся в противоположных направлениях, как в случае струны, закрепленной с обеих сторон. При этом необходимо учитывать следующее явление. После отражения от закрепленного конца отраженная деформация имеет противоположный знак. Это становится понятным, если учесть, что так, как смещение закрепленного конца все время отсутствует, у точки крепления развиваются силы, препятствующие приходящему изгибу струны. Эти силы порождают изгиб противоположного знака, начинающий распространяться в обратную сторону. Поэтому и в отраженной деформации знак смещения изменяется на обратный. Если отражается гармоническая волна, то такое изменение равносильно «потере» полуволны при отражении.
Таким образом, наложение двух волн даст следующее:
Используя формулу разности синусов, получим
.
(9.4)
Это выражение называется уравнением стоячей волны, при этом предполагается режим установившихся колебаний, то есть режим, возникающий после многократного пробега волн между креплениями струны. Из (9.4) видно, что в стоячей волне все точки среды (любое значение x ) колеблются по гармоническому закону с круговой частотой .
Амплитуда колебаний различна для разных точек и определяется из (9.4) следующим образом:
.
(9.5)
Из последнего выражения вытекает, что есть точки среды, называемые узлами, в которых колебания отсутствуют Z m = 0, следовательно, z = 0. Координаты этих точек определятся из условия равенства нулю синуса в выражении (9.5), то есть
.
(9.6)
Отсюда,
так как
,
получаем
.
Следовательно, расстояние между соседними узлами равно половине длины волны. Так как узлы все время остаются в покое, то в стоячей волне нет направленного переноса энергии, энергия не может перейти через узел. Передача энергии по струне производится только бегущей волной.
Те
точки, в которых значение амплитуды
достигает максимума
,
называются пучностями. Как следует из
выражения (9.5), координаты этих точек
определяются из условия
,
то есть отвечают уравнению
.
Видим, что расстояние между соседними
пучностями также равно половине длины
волны.
Множитель
при переходе через узел меняет знак,
вследствие чего фаза колебаний по разные
стороны от узла отличается на.
Все точки, находящиеся между двумя
соседними узлами, колеблются в одинаковой
фазе (их отклонения имеют одинаковый
знак). Условие неподвижности обоих
концов закрепленной струны приводит к
тому, что на длине струны должно
укладываться целое число полуволн:
.
(9.7)
Таким образом, стоячая волна образуется только при надлежащем соотношении размеров струны и длины волны (частоты колебаний). Для разных значений n = 1, 2,… получим различные типы, или моды, колебаний, при этом n определяет число пучностей, а не узлов. Из (9.6) с учетом (9.7) получим формулу для частот, при которых в струне устанавливаются стоячие волны
,
(9.8)
Частоты 
называют собственными частотами струны.
Частоту 
называют основной частотой, остальные
–
обертонами. Видим, что определяемые
формулой (9.8) собственные частоты не
зависят от модуля Юнга материала. Этот
результат является следствием того,
что мы пренебрегли изменением натяжения
струны при колебаниях.
В общем случае в струне могут одновременно существовать колебания с различными собственными частотами. Так, наряду с основным тоном n = 1, могут возбуждаться обертоны n = 2, 3, 4,….
Полученные выше уравнения описывают движение идеально гибкой струны в вакууме. При колебаниях реальной струны всегда происходят потери энергии.
Часть энергии теряется вследствие трения о воздух, другая часть уходит через концы струны и т.д. Для поддержания незатухающих колебаний служит вибратор. Если энергия потерь в точности компенсируется энергией, поступающей от вибратора, то в струне можно наблюдать стоячие волны. Но теперь по струне должна происходить передача энергии. Поэтому наряду со стоячими будут существовать бегущие волны, в результате чего узлы окажутся несколько размытыми. Если потери энергии за период малы по сравнению с запасом колебательной энергии в струне, то искажение стоячих волн бегущей волной будет незначительным.
Другим приближением в изложенной выше теории является пренебрежение неоднородностью струны. В реальной струне и плотность, и натяжение могут являться непрерывными функциями координаты Х . Например, если струна подвешена вертикально, то учет массы струны приведет к тому, что натяжение в верхних частях будет больше, чем внизу. Любая неоднородность приведет к искажению формы колебаний, так как синусоидальные колебания в пространстве характерны только для нормальных мод однородных систем.
